Unit 2: Teaching Motion

Inquiry-Oriented Student Performance Objectives:

2.1 Center of Mass:

1. Students will, given an irregularly shaped, 2-dimensional object, determine its center of mass.

2.2. Inertia:

1. Students will identify the parallel nature of linear and angular momentum and will come up with the following identities: F = ma corresponds to tau = I*alpha, v = r*omega, etc.
2. Students supplied with a meter stick and a variety of masses, will determine qualitatively the relationship between the moment of inertia, mass, and the distribution of that mass with respect to the fulcrum (e.g., the masses will be attached to corresponding points along a meter stick balanced at the center with the hand, and twisted from side to side to develop a qualitative assessment of the effect of mass and its distribution on the perceived moment of inertia).
3. Students, given the relationship tau = I*alpha, will use a rotational unit and appropriate computer software to determine the moment of inertia of several mass configurations to find relationship between the moment of inertia and the mass involved.
4. Students will use a rotational unit and appropriate computer software to determine the moment of inertia of several mass configurations to find relationship between the moment of inertia and the “orbital” radius of the mass involved.
5. Students will, given an incline and a large massive ball on a table, predict where a projectile will land on the floor taking into account potential, and both translational and rotational kinetic energies.

2.3 Velocity and Acceleration:

1. Students will design and conduct an experiment to collect and analyze suitable data to establish the general kinematics relationship:
2. Students will provide a theoretical explanation for the above empirical relationship; they will mathematically derive the relationship using the basic equation and the definitions of average (uniformly increasing) velocity and (constant) acceleration.
3. Students will interpret graphs relating d and t, v and t, and a and t for non-accelerated and uniformly accelerated objects.
4. Students will use a photogate, a free-falling picket fence, and appropriate computer software to determine the local value of the acceleration due to gravity.
5. Students will use an inclined plane, a dynamics cart, a photogate, and appropriate computer software to find the local value of the acceleration due to gravity incorporating appropriate use of vector-based force diagrams.

2.4 Periodic Motion:

1. Derive empirical principles for the factors observed to affect the period of a simple pendulum.
2. Use the above principles to conduct a dimensional analysis to find the theoretical relationship (a proportionality) between period and the relevant variables.
3. Design and conduct an experiment to verify the theoretical form of the simple pendulum period equation, and find the value of the constant of proportionality.
4. Determine the absolute and relative errors for pi expressed as (113/355)^-1. Note that the difference from pi in this relationship is 0.000000267 approximately.
5. Given the theoretical relationship for a simple pendulum,
   
   accurately determine the local value of the acceleration due to gravity. Calculate estimated absolute and relative errors. Hint: find and employ partial T/T.
6. In a properly controlled experiment, find the periods of a physical pendulum and a simple pendulum of the same length; compare; hypothesize what causes the difference.

2.5 Circular Motion:

Online Resources:

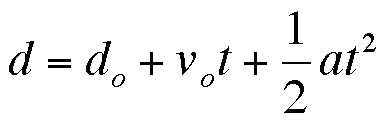
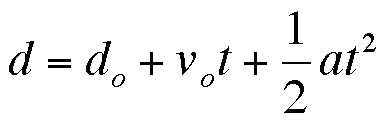
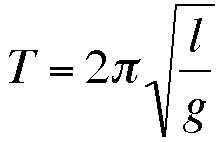
Hippocampus.org - see the numerous physics videos for every conceivable physics topic

Annenburg/CPB Video on Demand - see especially the 52-part series Mechanical Universe.

Here are some additional good to fair sites dealing with projectile motion furnished by Jason Ryan's Physics Class on November 7, 2002:

http://library.thinkquest.org/16600/games/bball/
This is a simple simulation where you try to get a basketball into the hoop by changing a few of the parameters.

http://www.explorescience.com/classic/monkey.htm
This is an adaptation to the shoot the monkey demo. Here you shoot a skeleton with a basketball.

http://zebu.uoregon.edu/nsf/cannon.html
This site has a little more with what you can do to the experiment. You can change gravity, the velocity, drag, …

http://www.phy.ntnu.edu.tw/java/projectile/projectile.html
This site has two cannons pointing at each other. The cannons shoot at the same time and you see the balls hit in the air. There wasn’t much that you could do with this one.

http://www.phys.virginia.edu/classes/109n/more_stuff/applets/projectilemotion/jarapplet.html
You can adjust the drag and other parameters on this site as well. I liked playing around here for a few minutes.

http://www.msu.edu/user/brechtjo/physics/cannon/cannon.html
This site is very simplistic. I didn’t stay here for too long.

http://plabpc.csustan.edu/java/projectiles/projectile.html
This site doesn’t let you see the projectile as it flies through the air. You just get to see where everything lands and the different distances.

http://home.a-city.de/walter.fendt/phe/projectile.htm
This is so far the best site that I have seen. There are many different components of the projectile that you can look at, force, energy, vectors…

http://library.thinkquest.org/15433/games/game3.htm
This site has a different type of game. You have to get a dog in a car to launch off a cliff into a cave.

http://members.bellatlantic.net/~vze23kcv/old/projectile.html
This is a list of projectile sites!!! Very helpful.

Return to PHY 312 course syllabus.