Research Interests

This is an investigation of transitions occurring in the dynamical states of pairs of distinct neurons electrically coupled, with one neuron tonic and the other bursting. Depending on the initial dynamical states of the two periodic neurons as individuals, for increasing values of the coupling strength, they synchronize through different transitions including chaos mediated by a period-doubling cascade. Increasing coupling strength eventually leads the two neurons back into periodic behavior, albeit different from their initial states. Certain intrinsic properties of the individual neurons such as minimum firing rates are carried over onto the dynamics of the coupled neurons, affecting their ultimate synchrony..

A. Shaffer, R. Follmann, A. Harris, S. Postnova, H. Braun, E. Rosa, Jr.,
    "A critical firing rate associated with tonic-to-bursting transitions in synchronized gap-junction coupled neurons,"
        Eur. Phys. J. ST 226, 1939 (2017).

A. Shaffer, A.L. Harris, R. Follmann, and E. Rosa, Jr.,
       "Bifurcation Transitions in Gap-Junction-Coupled Neurons,"
        Phys. Rev. E 94, 042301 (2016).

Central pattern generators are neuron networks that produce vital rhythmic motor outputs such as those observed in mastication, walking and breathing. Their activity patterns depend on the tuning of their intrinsic ionic conductances, their synaptic interconnectivity and entrainment by extrinsic neurons. The infuence of two commonly found synaptic connectivities { reciprocal inhibition and electrical coupling { are investigated here using a neuron model with subthreshold oscillation capability, in different coupling and entrainment regimes. We study the dynamics displayed by a network of a pair of neurons with various ring regimes, coupled by either (i) only reciprocal inhibition or by (ii) electrical coupling first and then reciprocal inhibition. In both scenarios a range of coupling strengths for the reciprocal inhibition is tested, and in general the neuron with the lower compling rate stops spiking for strong enough inhibitory coupling, while the faster neuron remains active. However, in scenario (ii) the originally slower neuron stops spiking at weaker inhibitory coupling strength, suggesting that the electrical coupling introduces an element of instability to the two-neuron network..

E. Rosa, Jr., Q. Skilling, and W. Stein
       "Effects of Reciprocal Inhibitory Coupling in Model Neurons,"
       Biosystems 127, 73-83 (2015).

Long-range communication in the nervous system is usually carried out with the propagation of action potentials along the axon of nerve cells. While typically thought of as being unidirectional, it is not uncommon for axonal propagation of action potentials to happen in both directions. This is the case because action potentials can be initiated at multiple ectopic positions along the axon. Two ectopic action potentials generated at distinct sites, and traveling toward each other, will collide. As neuronal information is encoded in the frequency of action potentials, action potential collision and annihilation may affect the way in which neuronal information is received, processed, and transmitted. We investigate action potential propagation and collision using an axonal multicompartment model based on the Hodgkin-Huxley equations.We characterize propagation speed, refractory period, excitability, and action potential collision for slow (type I) and fast (type II) axons. In addition, our studies include experimental measurements of action potential propagation in axons of two biological systems. Both computational and experimental results unequivocally indicate that colliding action potentials do not pass each other; they are reciprocally annihilated. .

R. Follmann, E. Rosa, Jr., and W. Stein,
       "Dynamics of Signal Propagation and Collision in Axons,"
       Phys. Rev. E 92, 032707 (2015).

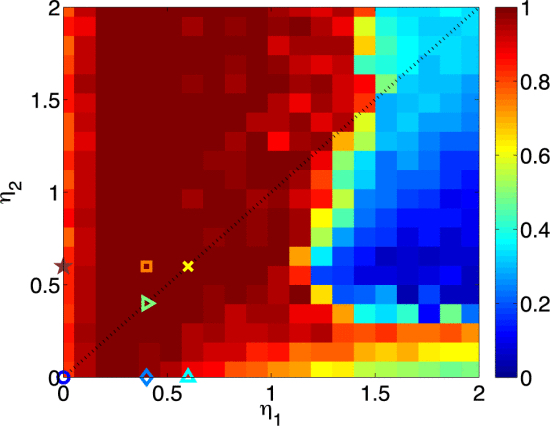The understanding of the underlying mechanisms for information processing and representation in the brain is a topic of central interest in neuroscience. A properly interconnected set of Kuramoto-type oscillators is used in a new associative-memory network configuration, which includes second and third order terms in the Fourier expansion of the network coupling. Investigation of the response of the network to different external stimuli indicates an increase in the network capability for coding and information retrieval. Comparison of the network output with that of an equivalent experiment with subjects, for recognizing perturbed binary patterns, shows comparable results between the two methods. The enhanced storage capacity of the network is also discussed. .

R. Follmann, E. E. N. Macau, E. Rosa, Jr., and J. R. C. Piqueira,
       "Phase Oscillatory Network and Visual Pattern Recognition,"
       IEEE Trans Neural Networks Learning Systems 26, 1539-44 (2015).