Full window version
(looks a little nicer). Click <Back> button to get back to
small framed version with content indexes.
This material (and images) is copyrighted!. See my copyright notice for fair use practices.
This chapter covers the
revolutionary advancements due to probably the most
brilliant scientist who ever lived: Isaac Newton (lived 1641--1727).
His greatest contributions
were in all branches of physics. Kepler's discoveries about elliptical orbits and
the planets' non-uniform
speeds made it impossible to maintain the idea of planetary motion as a natural one
requiring no explanation. Newton had to answer some basic questions: What keeps the
planets in their elliptical orbits? On our spinning Earth what prevents objects
from flying away when they are thrown in the air? What keeps you from being hurled
off the spinning Earth? Newton's answer was that a fundamental force called
``gravity'' operating between all objects made them move the way they do.
Newton developed some basic rules governing the motion of all objects. He used
these laws and Kepler's laws to derive his unifying Law of Gravity. I will first
discuss his three laws of motion and then discuss gravity. Finally, several
applications in astronomy will be given. This chapter uses several math concepts
that are reviewed in the mathematics review appendix.
If your math skills are rusty, study the
mathematics review appendix and don't hesitate to
ask your astronomy instructor for help. The vocabulary terms are in boldface.
I include images of world atlases from different time periods in this chapter
and the previous one as another way to illustrate the advances in our understanding of
our world and the universe. Links to the sites from which the photographs came
are embedded in the images. Select the picture to go to the site.
Nova orbis tabula [De Wit 1688]. Select the image to go to the Hargrett Library
at the Univ. of Georgia from which this picture came. Note the curved path of
the Sun between the Tropic of Cancer (at latitude 23.5ƒ N) and the Tropic
of Capricorn (at latitude 23.5ƒ S).
In order to accurately describe how things move, you need to be careful in how
you describe the motion and the terms you use. Scientists are usually very careful
about the words they use to explain something because they want to accurately
represent nature. Language can often be imprecise and as you know, statements can
often be misinterpreted. Because the goal of science is to find the single true
nature of the universe, scientists try to carefully choose their words to accurately
represent what they see. That is why scientific papers can look so ``technical''
(and even, introductory astronomy textbooks!)
When you think of motion, you may first think of something moving at a uniform
speed. The speed = (the distance travelled)/(the time it takes). Because
the distance is in the top of the fraction, there is a direct relation between the
speed and the distance: the greater the distance travelled in a given time, the
greater is the speed. However, there is an inverse relation between time and speed
(time is in the bottom of the fraction): the smaller the time it takes to
cover a given distance, the greater the speed must be.
To more completely describe all kinds of changes in motion, you also need to consider
the direction along with the speed. For example, a ball thrown upward at the
same speed as a ball thrown downward has a different motion. This inclusion of
direction will be particularly important when you look at an object orbiting a planet
or star. They may be moving at a uniform speed while their direction is constantly
changing. The generalization of speed to include direction is called
velocity. The term velocity includes both the
numerical value of the speed and the direction something is moving.
Galileo conducted
several experiments to
understand how something's velocity can be changed. He found that an object's
velocity can be changed only if a force acts on the object. The philosopher
RenÈ Descartes (lived 1596--1650, picture at left) used the idea
of a greater God and an
infinite universe with no special or privileged place to articulate the concept of
inertia: a body at rest remains at rest, and
one moving in a straight line maintains a constant speed and same direction unless
it is deflected by a ``force''. Newton took this as the beginning of
his description of how things move, so this is now known as Newton's 1st law
of motion. A force causes a change in something's
velocity (an acceleration).
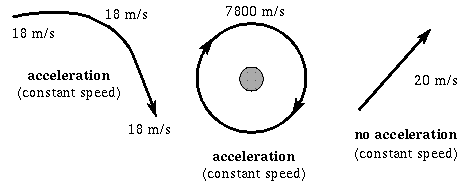
An acceleration is a change in the speed and/or
direction of motion in a given amount of time: acceleration= (the velocity
change)/(the time interval of the change).
Something at rest is not accelerating and something moving at constant speed in
a straight line is not accelerating. In common usage, acceleration usually means
just a change in speed, but a satellite orbiting a planet is
constantly being accelerated even if its speed is constant because its
direction is constantly being deflected. The satellite must be experiencing a force
since it is accelerating. That force turns out to be gravity. If the force (gravity)
were to suddenly disappear, the satellite would move off in a straight line along
a path tangent to the original circular orbit.
A rock in your hand is moving horizontally as it spins around the center of
the Earth, just like you
and the rest of the things on the surface are. If you throw the rock straight up,
there is no change in its horizontal motion because of its inertia. You
changed the rock's vertical motion because you applied a vertical force
on it. The rock falls straight down because the Earth's gravity acts on only
the rock's vertical motion. If the rock is thrown straight up, it does not
fall behind you as the Earth rotates. Inertia and gravity also explain why you do
not feel a strong wind as the Earth spins---as a whole, the atmosphere is spinning
with the Earth.
Newton's first law of motion is a qualitative one---it
tells you when something will accelerate.
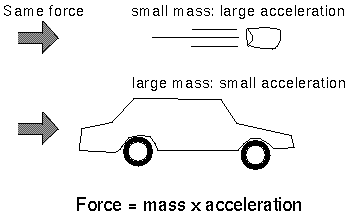
Newton went on to quantify the amount of the change that would be observed
from the application of a given force. In
Newton's second law of motion, he said that
the force applied = mass of an object × acceleration.
Mass is the amount of material an object has and is a way
of measuring how much inertia the object has.
For a given amount of force, more massive objects
will have a smaller acceleration than less massive objects (a push needed to even
budge a car would send a pillow flying!). For a given amount of acceleration, the
more massive object requires a larger force than a less massive object.
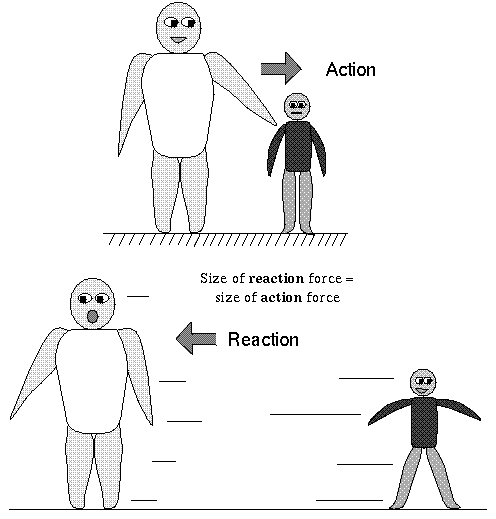
Newton also found that for every action force ON an object, there
is an equal but opposite force BY the object
(Newton's third law of motion). For example, if Andre
the Giant is stuck on the ice
with Tom Thumb and he pushes Tom Thumb to the right, Andre will feel an equal force
from Tom pushing him to the left. Tom will slide to the right with great speed and
Andre will slide to the left with smaller speed since Andre's mass is larger than
Tom's.
Another example: an apple falls to the Earth because it is
pulled by the force of the Earth's gravity on the apple and the acceleration of the
apple is large. The apple also exerts a gravitational force on the Earth of the
same amount. However, the acceleration the Earth experiences is
vastly smaller
than the apple's acceleration since the Earth's mass is vastly larger than the
apple's---you will ordinarily refer to the apple falling to the Earth, rather than the
Earth moving toward the apple or that they are falling toward each other.
Vocabulary
| acceleration | force | inertia |
| mass | Newton's 1st law |
Newton's 2nd law |
| Newton's 3rd law | velocity |
Formulae
Newton's 2nd law: Force = mass × acceleration: F = m × a
- What 2 things can change for an acceleration?
- If you give a bowling ball a push FAR away from any gravitational effects,
what will it do? If you throw a feather (again far out in space) at the same
speed as the bowling ball, how will its speed compare to the bowling ball
after 5 minutes?
- Let's say you're twirling a ball on a string and the string breaks. What
path does the ball take and why is that?
- How do you know gravity acts on an orbiting satellite?
- How does a force exerted on an object relate to the object's mass or
acceleration? Given the same force will a boulder accelerate more than a
regular marble? Why?
- Why would you need to apply more force to a bowling ball than a feather (far
out in space) so that they
would be travelling at the same speed after 10 minutes?
Using Kepler's third law and his own second law, Newton found that the amount
of the attractive
force, called gravity, between a planet and Sun a distance d apart is Force
= kp × (planet mass) /
(d)2, where kp is a number that is the
same for all the planets. In the same way he found that the amount of the
gravity between the Sun and a planet is Force = ks × (Sun mass) /
(d)2. Using
his third law of motion, Newton reasoned that these forces must be the same (but
acting in the opposite directions). He derived his Law of Gravity: the
force of gravity = G × (mass #1) × (mass #2) /
(distance between them)2 and this force is directed toward
each object, so it is always attractive. The term G is a universal constant
of nature. If you use the units of
kilograms (kg) for mass and meters (m) for distance, G = 6.672 × 10-11
m3 /(kg sec2). If you need a refresher on exponents, square
& cube roots, and scientific
notation, then please study the math review appendix.
Spherically
symmetric objects (eg., planets, stars, moons, etc.) behave as if all of their mass
is concentrated at their centers. So when you use Newton's Law of Gravity, you
measure the distance between the centers of the objects.
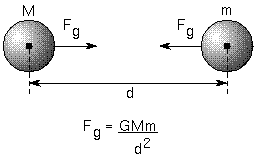
In a bold, revolutionary step, Newton stated that his gravity law worked for
any two objects with mass---it applies for any motions on the Earth, as well
as, any motions in space. He unified celestial and terrestrial physics and completed
the process started by Copernicus of removing the Earth from a unique position or
situation in the universe. His law of gravity also explained Kepler's 1st and
2nd laws.
Newton's Law of Gravity says a lot about this force in a very compact, elegant way.
It says that any piece of matter will feel it whether it is charged or not (this
sets it apart from electrical and magnetic forces that affect only charged objects).
Gravity depends only the masses of the two attracting objects and their distance from
each other. It does not depend on their chemical composition or density. A glob of
peanut butter the mass of the Sun will have the same gravitational effect on the
Earth as the Sun does. Gravity is always attractive, never repulsive (this is another
way it is different from electrical and magnetic forces).
Because the masses are in the top of the fraction, more mass creates more gravity force.
This also means that more massive objects produce greater accelerations
than less massive objects. Since distance is in the bottom of the fraction, gravity has
an inverse relation with distance: as distance increases, gravity
decreases. However, gravity never goes to zero---it has an infinite range (in
this respect it is like the electrical and magnetic forces). Stars feel the gravity
from other stars, galaxies feel gravity from other galaxies, galaxy clusters feel
gravity from other galaxies, etc. The always attractive gravity can act over the
largest distances in the universe.
There is no way to
get rid of the force of gravity. If you want to prevent a body from
producing a
gravitational acceleration on
an object, you need to use a second body, with the same amount of gravity pull
as the first body, in a way that its gravity pulling on the object is in the
opposite direction. The resulting accelerations due to the forces
from the two bodies will cancel each other out.
- What basic fundamental assumption did Newton make about the laws of
nature on the Earth and in space?
- Why is gravity often the most important force in astronomical
interactions?
- What things does gravity depend on?
- How does gravity vary with distance between objects and with respect to
what do you measure the distances?
- What would happen to the orbit of Io (one of Jupiter's moons) if all of
the Hydrogen and Helium in Jupiter were converted to Silicon and Oxygen? Explain your
answer.
- What would happen to the Earth's orbit if the Sun suddenly turned into a
black hole (of the same mass)? Why?
- How would antimatter respond to gravity? (Hint: antimatter
has mass just like ordinary matter.)
- What important laws of planet motion can be derived from Newton's law
of gravity?
Though the terms weight and mass are used interchangeably in
common language, in science there is distinct difference between the two terms. The
weight of an object = force of gravity felt by that object but the
mass of
an object is the amount of matter the object has. Mass is a measure of the
object's resistance to acceleration: a push on a skateboard will make it roll
away quickly but the same push on a more massive car will barely budge it.
An object's weight depends on the pull of the
gravitating object but the object's mass is independent of the gravity. For
example, Joe Average weighs himself on the Earth's surface and then on the Moon's
surface. His weight on the Moon will be about six times less than on the
Earth but the number of atoms in his body has not changed so his mass is
the same at the two places. In the old English unit system, there is a
``pound'' of force and ``pound'' of mass. On only the Earth's
surface, an object's pound of mass = the number
of pounds of force felt by the object due to the Earth's gravity.
In the metric system there is no confusion of terms. A kilogram is a
quantity of mass and a newton is a quantity of force. One
kilogram (kg) = 2.205 pounds of mass and 4.45 newtons (N) = 1 pound of force. If
someone uses ``pounds'', be
sure you understand if s/he means force or mass!
How do you do that?
To find something's weight in
newtons, you multiply the mass in kilograms by the acceleration of gravity in the
units of meters/seconds2. For example: Joe Average has a mass
of 63.5 kg and
he feels a force of gravity on the Earth = 63.5 kg × 9.8 m/s2 =
623 kg m/s2 = 623 N.
His weight is 623 N. The other value in the preceding equation, 9.8
m/s2, is the acceleration due to gravity close to the Earth's surface.
Joe Average's weight at other places in the universe will be different
but his mass will remain the same.
|
Vocabulary
| kilogram | mass | newton |
| weight |
- What is the difference between mass and weight?
- When the astronauts landed on the Moon, how were they able to stay on the
ground?
- On the Moon, the astronauts weighed about six times less than they did on
the Earth. Compare the amount of gravity on the Moon's surface with that on the
Earth's surface. If objects fall with an acceleration of about 10 m/s2 on the
Earth, how much would the acceleration be on the Moon's surface? Explain
your answer.
- If Joe Astronaut has a mass of 40 kilograms on the Earth, how much mass would
he have on an asteroid with 10 times less surface gravity than the Earth's surface
gravity? Explain your answer.
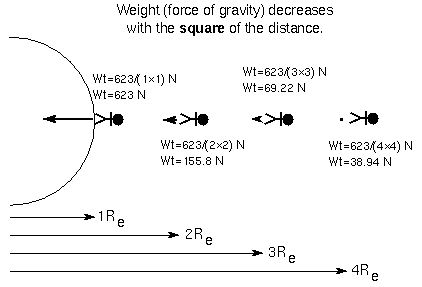
Newton's law of gravity describes a force that decreases with the SQUARE of
the distance. For every factor of 2 the distance increases, the gravitational
attraction decreases by a factor of 2 × 2 = 4; for every factor of
3 increase in distance, the gravity decreases by a factor of 3 × 3 = 9
(not by 3 + 3 = 6!); for every factor of 4 increase in distance, the gravity
decreases by a factor of 4 × 4 = 16 (not by 4 + 4 = 8!), etc. See the
mathematics review appendix for a review
of ``factor'' and ``times''. Some more examples are given in the table below. Notice
how quickly an inverse square law gets very small.
A comparison of inverse and inverse square relations
| distance | inverse | inverse square |
| 1 | 1/1 = 1 | 1/12 = 1 |
| 2 | 1/2 = 0.5 | 1/22 = 1/4 = 0.25 |
| 3 | 1/3 = 0.33 | 1/32 = 1/9 = 0.11 |
| 4 | 1/4 = 0.25 | 1/42 = 1/16 = 0.0625 |
| 7 | 1/7 = 0.14 | 1/72 = 1/49 = 0.02 |
| 10 | 1/10 = 0.1 | 1/102 = 1/100 = 0.01 |
| 100 | 1/100 = 0.01 | 1/1002 = 1/10,000 = 0.0001 |
Example: Joe Average has a mass of 63.5 kilograms, so he weighs 623 newtons
(=140 pounds) on
the Earth's surface.
If he moves up 1 Earth radius (= 6378 kilometers) above the surface, he will
be two
times farther away from the Earth's center (remember that distances are
measured from center-to-center!), so his weight will be four times
less, or 623/4 newtons = 155.8 newtons (= 140/4 pounds); NOT two times less,
or 623/2 newtons = 311.5 newtons. If he moves up another Earth
radius above the surface, he will be three times farther away than he was at the
start, so his weight will drop by a factor of nine times, NOT 3 times. His
weight will be 623/9 newtons = 69.22 newtons (= 140/9 pounds); NOT 623/3
newtons = 207.7 newtons. His mass will
still be 63.5 kilograms. Figure below illustrates this.
Let us generalize this for any situation where the masses do not change:
the force of gravity at distance A = (the force of gravity at distance B) ×
(distance B / distance A)2. Notice which distance is in the top of the
fraction! To use
this relation, have the gravity at distance A represent the unknown gravity force
you are trying to find and the gravity at distance B represent the reference
gravity force felt at the reference distance B.
How do you do that?
Let's find where the weight values in the inverse square law figure come from.
For Mr. Average's case the reference weight is his
weight on the surface of the Earth = 623 N. His
weight at 6378 kilometers above the surface is
gravity at A = 623 × [6378/(2 × 6378)]2 = 623 ×
1/22 = 623 × 1/4 = 155.8 N.
When he is at two Earth radii above the
surface, the gravity at A = 623 × [6378/(3 × 6378)]2 = 623 ×
1/32 = 623 × 1/9 = 69.22 N.
|
Formulae
Inverse Square Law: Gravity at A = gravity at B × (distance B /
distance A)2.
- Why is gravity called an ``inverse square law''?
- What is the difference between a simple inverse relation and an inverse
square relation?
- If the Earth was 3 A.U. from the Sun (instead of 1 A.U.), would the gravity
force between the Earth and the Sun be less or more than it is now? By how many
times?
- If Mercury was 0.2 A.U. from the Sun (instead of 0.4 A.U.), would the gravity
force between Mercury and the Sun be less or more than it is now? By how many times?
Galileo found that the acceleration due to gravity (called ``g'') depends only on
the mass of the
gravitating object and the distance from it. It does not depend on the mass of
the object being pulled. In the absence of air drag, a huge boulder will fall at
the same rate as a small
marble dropped from the same height as the boulder. A tiny satellite at
the same distance from the Sun as Jupiter's orbit from the Sun
feels the same acceleration from the Sun as the large planet
Jupiter does from the Sun.
How is this possible? Most people would agree with Aristotle that the bigger object
should fall faster than the smaller object, but experiments show they would be wrong.
A boulder
falling toward the Earth is pulled by a
stronger gravity force than the marble, since the boulder's mass is greater
than the marble, but the boulder also has greater resistance to a change in its
motion because of its larger mass. The effects cancel each other out, so the
boulder accelerates at the same rate as the marble. The same line of
reasoning explains the equal acceleration experienced by Jupiter and the satellite.
You can use Newton's second law of motion F = m × a (which relates the
acceleration, a, felt by a object with mass m when acted on by a force
F) to derive the acceleration due to gravity (here replace a
with g) from a massive object:
| The force of gravity = |
| = m g |
| so |
|
|
| g = |
| . |
The gravitational acceleration depends on only the mass of the gravitating object
M
and the distance d from it. Notice that the mass of the falling object m has
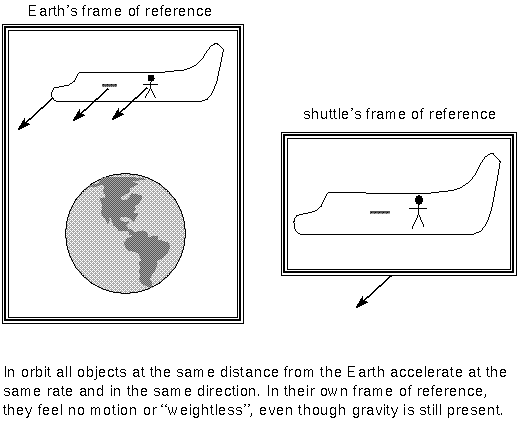
been cancelled out. This explains why astronauts orbiting the Earth feel ``weightless''.
In orbit they are continually ``falling'' toward the
Earth because of gravity (the Earth's surface curves away from them at the same
rate they are moving forward). If Jane Astronaut drops a pen in the space shuttle,
it accelerates toward the Earth, but she accelerates by the same amount so the
pen remains at the same position relative to her. In fact the entire shuttle and
its contents are accelerating toward the Earth at the same rate, so Jane and her
companions ``float'' around inside! This is because all of them are at very
nearly the same distance from the Earth.
The acceleration decreases with the SQUARE of the
distance (inverse square law). To compare gravity accelerations due to the
same object at different distances, you use the gravity acceleration g at
distance A = (the gravity acceleration g at distance
B) × (distance B / distance A)2. Notice which distance
is in the top of the fraction. An example of using the inverse square law
is given in the ``How do you do that?'' box below.
How do you do that?
Find how many times more gravitational acceleration the Galileo
atmosphere probe felt at 100,000 miles from Jupiter's center than the orbiter
felt at 300,000 miles. You have
| probe's g | = orbiter's g ×
(300,000/100,000)2 = orbiter's g × (3/1)2 |
| = orbiter's g × 9. |
The probe accelerated by an amount nine times greater than the orbiter.
|
Measuring the acceleration of an object dropped to the ground enables you to
find the mass of the Earth. You can rearrange the gravity acceleration relation
to solve for the mass M to find M = g d2/G. Close to the
Earth's surface at a distance of 6.4 × 106 meters from the center,
g = 9.8 m/s2. The distance is given in meters to match the units of the
gravity acceleration---when you do a calculation, you must be sure you check that
your units match up or you will get nonsense answers. The big G is the universal
gravitational constant, approximately 6.7×10-11 m3/(kg sec2).
Plugging in the values, you will find the Earth's mass = 9.8 ×
(6.4×106)2 / (6.7 × 10-11) kilograms =
6.0 × 1024 kilograms. If you are unsure of how to work with scientific
notation, read the scientific notation
section in the mathematics review appendix
(pay close attention to the part
describing how to enter scientific notation on your calculator!).
You can
determine masses of stars and planets in
a similar way: by measuring the acceleration of objects orbiting them and
the distance between the star or planet and the object. A small object falling to the
Earth has mass and, therefore, has a gravitational acceleration associated
with it: the Earth is accelerated toward the falling object (an example of
Newton's third law)! However, if you
plug some typical masses of terrestrial objects (less than, say, 1000 kilograms)
into the acceleration formula,
you will see that the amount the Earth is accelerated is vastly smaller than
the falling object's acceleration. You can ignore the Earth's acceleration.
A side note: determining the mass of the Earth also depends on knowing the
value of the gravitational constant G. The constant was first measured by
Henry Cavendish in 1798. After discussing his experimental results, he then
applied his measurement to the subject of his paper's title: ``Weighing the
Earth.''
Formulae
- Gravitational Acceleration: g = (G × Mass)/(distance from the center)2.
- Comparing gravitational accelerations: acceleration at position A = acceleration at
position B × (distance B/distance A)2.
- Calculating mass: Mass = (g × distance2)/G.
- What did Galileo discover about how objects of different masses fall to the
Earth?
- If you dropped a hammer and feather from the same height above the Earth's
surface, which would actually hit the ground first? Why would it be different than
what Galileo said about falling objects? Explain why if you let the feather fall quill
end first, the result is closer to what Galileo said.
- If you dropped a hammer and feather from the same height above the airless
Moon's surface, which would actually hit the ground first? Explain why your
answer is different than for the previous question.
- How many times less/more gravity acceleration due to the Sun does the
Ulysses spacecraft feel at 2.3 A.U. above the Sun than the solar gravity
acceleration it felt at Jupiter (5.2 A.U. from the Sun)? Is it accelerated more
or less at 2.3 A.U. than when it was at 5.2 A.U.?
- Why do astronauts in orbit around the Earth feel ``weightless'' even though
the Earth's gravity is still very much present?
- Put the following in order of their acceleration around the Earth: a 200-ton
space station 6580 kilometers from the center, a 60-kilogram astronaut
6580 kilometers
from the center, a 1-ton satellite 418,000 kilometers from the center, and the
7.4×1019-ton Moon 384,000 kilometers from the center. Explain your answer.
- How can you find the mass of the Earth using ordinary objects in your house?
Newton found that his gravity
law is obeyed everywhere in the universe and could explain Kepler's three laws of orbital
motion. Newton's development
of the unifying law of gravity was also the culmination of a process of Occam's
Razor in action. From Ptolemy to Newton, the theories of how the planets move
got simpler and more powerful as time went on. Ptolemy's model had become
extremely complicated by the time of the Renaissance and Copernicus reduced the
number of circular motions to around 50 so it was simpler to use. Kepler vastly
simplified the theory of planet motion by reducing the number of essential parts
to just three laws. Newton unifed all of those laws to the ONE unifying law of
gravity. This law was so simple and elegant that it could also explain motions on
the Earth.
But what is gravity? Newton understood how the
gravity force affected the motion of objects but not why gravity worked the way it
did. Recognizing the limits of his knowledge, he adopted an
instrumentalist view: the scientist's job is to capture observations in precise
mathematical equations; explain the ``how'' not the ``why''. Only things
verified by our experience of the world are admissible into science. Though the
``why'' question is intriguing and a few scientists will spend years trying to
answer it, most scientists share Newton's instrumentalist view.
With Newton, there was no longer a
hierarchical-teleological universe (one designed by God for some purpose with man
playing a crucial role in the plan). The universe was now a perfect machine, based
on mathematics, set in motion by God
long ago. God is the reference point for absolute space and time. Newtonian
mechanics requires an absolute coordinate system to keep things sensible (according to
Newton this
also gave God something to do).
With the success of Newton's ideas, a major change occurred
in how people viewed the
world around them. Reality was completely reduced to material objects.
Ideas, thought, feelings, and values were secondary. Newtonism undercut the
role of God and religion and the validity of science: science became just a
subjective perspective of the machine universe.
Descartes saw the need to rescue thoughts, ideas and
values. He developed a mind-body dualism: a world of thought and spirit exists
independent of, but parallel to, the material world. There is a correspondence
between the God-inaugurated, mathematical thoughts of scientists and the
motions in the physical world. Descartes said that mathematical ideas work so
well because there is a pre-established parallelism between the physical world
and the human mind. What is real does NOT depend on us---this is probably
the actual completion of the Copernican revolution and was soon so
widely accepted that it became ``common sense'' (how about that for a paradigm shift!).
- What important discoveries and ideas did Newton make?
- How does Occam's Razor relate to the progress of planet motion theory
from Ptolemy to Newton?
- How can Newton's work be considered the completion of the process started
by Copernicus almost 120 years earlier?
Go to
Orbits and Tides sections
last updated 25 January 1999
Nick Strobel --
Email:
strobel@lightspeed.net
(661) 395-4526
Bakersfield College
Physical Science Dept.
1801 Panorama Drive
Bakersfield, CA 93305-1219