History and Philosophy of Western Astronomy

Full window version (looks a little nicer). Click <Back> button to get back to small framed version with content indexes.

This chapter covers the development of western astronomy and modern science. I focus on the rise of modern science in Europe, from the ancient Greeks to Isaac Newton. Other cultures were also quite interested and skilled in astronomy (the Mayans, Egyptians, peoples of India and China come immediately to mind), but the Greeks were the first ones to try to explain how the universe worked in a logical, systematic manner using models and observations. Modern astronomy (and all of science) has its roots in the Greek tradition. If you would like a more thorough discussion of the history of astronomy than what I will present here, please take a look at Science and the Human Prospect by Ronald Pine. I will give dates of when certain persons lived and worked to give you some reference points in the long history of astronomy. Don't worry about memorizing the dates. What is more important is to see the development of ideas and methods of modern science.

I include images of world atlases from different time periods in this chapter and the next as another way to illustrate the advances in our understanding of our world and the universe. Links to the sites from which the photographs came are embedded in the images. Select the picture to go to the site. The vocabulary terms are in boldface.

Philosophical Backdrop

Ancient Greece's view of their world. Select the image to go to Jim Siebold's ancient maps database from which this picture came.

By the 7th Century B.C.E. a common viewpoint had arisen in Greece that the Universe is a rational place following universal, natural laws and we are able to figure out those laws. Open inquiry and critical evaluation was highly valued. The emphasis was on the process of learning about the universe rather than attaining the goal. But people eventually got tired of learning and wanted absolute answers. Science is not able to give absolute, certain answers. There was disagreement among the experts and there came to be a crisis in confidence that led to the rise of the Sophists.

The Sophists taught that an absolute truth and morality are myths and are relative to the individual. Since truth and morality were just cultural inventions for the Sophists, they said a person should conform to the prevailing views, rather than resolutely holding to some belief as an absolute one. Socrates (lived 470--399 B.C.E.) disagreed with the Sophists, teaching that we can attain real truth through collaboration with others. By exploring together and being skeptical about ``common sense'' notions about the way things are, we can get a correct understanding of how our world and society operate. This idea of being skeptical so that a truer understanding of nature can be found is still very much a part of modern science.

Socrates' student, Plato(lived 427--347 B.C.E.), developed Socrates' ideas further. Plato taught that there are absolute truths---mathematics is the key. While statements about the physical world will be relative to the individual and culture, mathematics is independent of those influences: 2 + 2 = 4 always, here on Earth or on the far side of the galaxy. Plato had Four Basic Points:

1. There is certainty.
2. Mathematics gives us the power of perception.
3. Though the physical applications of mathematics may change, the thoughts themselves are eternal and are in another realm of existence.
4. Mathematics is thought and, therefore, it is eternal and can be known by anyone. [Today we view mathematical ideas as free creations of the human mind. They are the tools we use to map the world. Experience is the key. Although absolute certainty is not possible, we can still attain accurate knowledge and reasonable beliefs about the world.]

Out of Plato's teachings grew the belief that when one studies mathematics, one studies the mind of God. Mathematical symmetries are the language of universal design and harmony. Their faith in order caused the Greeks to try to find explanation for the seemingly unordered planets (particularly retrograde motion). Their faith in an ordered universe compelled them to make precise observations and they were sustained by their belief in the power of reason. In one form or another, modern scientists have this faith in an ordered universe and the power of human reason.

The Greeks were guided by a paradigm that was first articulated by Pythagoras (picture on left) before Socrates' time. A paradigm is a general consensus of belief of how the world works. It is a mental framework we use to interpret what happens around us. It is what could be called ``common sense''. The Pythagorean Paradigm had three key points about the movements of celestial objects:

1. The planets, Sun, Moon and stars move in perfectly circular orbits;
2. The speed of the planets, Sun, Moon and stars in their circular orbits is perfectly uniform;
3. The Earth is at the exact center of the motion of the celestial bodies.

Plato's Homework Problem

Some of the observations that convinced the Greeks that the Earth was not moving are

1. The Earth is not part of the heavens. Today the Earth is known to be just one planet of nine that orbit an average star in the outskirts of a large galaxy, but this idea gained acceptance only recently when telescopes extended our vision.
2. The celestial objects are bright points of light while the Earth is an immense, nonluminous sphere of mud and rock. Modern astronomers now know that the stars are objects like our Sun but very far away and the planets are just reflecting sunlight.
3. The Greeks saw little change in the heavens---the stars are the same night after night. In contrast to this, they saw the Earth as the home of birth, change, and destruction. They believed that the celestial bodies have an immutable regularity that is never achieved on the corruptible Earth. Today astronomers know that stars are born and eventually die (some quite spectacularly!)---the length of their lifetimes are much more than a human lifetime so they appear unchanging. Also, modern astronomers know that the stars do change positions with respect to each other over, but without a telescope, it takes hundreds of years to notice the slow changes.
4. Finally, our senses show that the Earth appears to be stationary! Air, clouds, birds, and other things unattached to the ground are not left behind as they would be if the Earth was moving. There should be a strong wind if the Earth were spinning as suggested by some radicals. There is no strong wind. If the Earth were moving, then anyone jumping from a high point would hit the Earth far behind from the point where the leap began. Furthermore, they knew that things can be flung off an object that is spinning rapidly. The observation that rocks, trees, and people are not hurled off the Earth proved to them that the Earth was not moving. Today we have the understanding of inertia and forces that explains why this does not happen even though the Earth is spinning and orbiting the Sun. That understanding, though, developed about 2000 years after Plato.

Plato taught that since an infinite number of theories can be constructed to account for the observations, we can never empirically answer what the universe is really like. He said that we should adopt an instrumentalist view: scientific theories are just tools or calculation devices and are not to be interpreted as real. Any generalizations we make may be shown to be false in the future and, also, some of our false generalizations can actually ``work''--an incorrect theory can explain the observations (see the scientific method page for background material on this).

Aristotle (lived 384--322 B.C.E.) was a student of Plato and had probably the most significant influence on many fields of studies (science, theology, philosophy, etc.) of any single person in history. He thought that Plato had gone too far with his instrumentalist view of theories. Aristotle taught a realist view: scientific, mathematical tools are not merely tools---they characterize the way the universe actually is. At most one model is correct. The model he chose was one developed by another follower of Plato, Eudoxus. The planets and stars were on concentric crystalline spheres centered on the Earth. Each planet, the Sun, and the Moon were on their own sphere. The stars were placed on the largest sphere surrounding all of the rest.

Aristotle chose this model because most popular and observational evidence supported it and his physics and theory of motion necessitated a geocentric (Earth-centered) universe. In his theory of motion, things naturally move to the center of the Earth and the only way to deviate from that is to have a force applied to the object. So a ball thrown parallel to the ground must have a force continually pushing it along. This idea was unchallenged for almost two thousand years until Galileo showed experimentally that things will not move or change their motion unless a force is applied. Also, the crystalline spheres model agreed with the Pythagorean paradigm of uniform, circular motion (see the previous section).

Astronomers continued working on models of how the planets moved. In order to explain the retrograde motion some models used epicycles---small circles attached to larger circles centered on the Earth. The planet was on the epicycle so it executed a smaller circular motion as it moved around the Earth. This meant that the planet's distance from us changed and if the epicyclic motion was in the same direction (e.g., counter-clockwise) as the overall motion around the Earth, the planet would be closer to the Earth as the epicycle carried the planet backward with respect to the usual eastward motion. This explained why planets are brighter as they retrogress.

Ptolemy's view of the world. Select the image to go to Jim Siebold's ancient maps database from which this picture came.

Ptolemy's geocentric universe

Select image to show animation of retrograde motion.

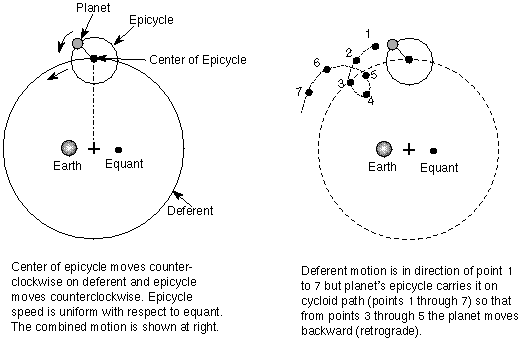
These refinements were incompatible with Aristotle's model and the Pythagorean paradigm---a planet on an epicycle would crash into its crystalline sphere and the motion is not truly centered on the Earth. So Ptolemy adopted an instrumentalist view---this strange model is only an accurate calculator to predict the planet motions but the reality is Aristotle's model. This apparent contradiction between reality and a calculation device was perfectly fine in his time. Our modern belief that models must characterize the way the universe actually is is a tribute to the even longer-lasting influence of Aristotle's realism. Ptolemy was successful in having people adopt his model because he gathered the best model pieces together, used the most accurate observations and he published his work in a large 13-volume series called the ``Almagest'', ensuring that his ideas would last long after he died.

Go to Renaissance Astronomy section

Go to Astronomy Notes beginning

Go to Astronomy 1 homepage

last updated 25 January 1999