Now that you have some feeling for the scales of time and space that astronomy encompasses and some of the difficulties caused by being Earth-bound (well, okay: solar-system bound!), let's take a look at what is up there in the sky beyond the clouds. In this chapter, you will learn where to find the key points on the night sky, how to use the coordinate system that astronomers use, how the Sun's position among the stars changes and how that affects the temperature throughout the year, and about the phases of the Moon and eclipses. At the end of chapter, you will learn about the motions of the planets among the stars. All of the things in this chapter, you can observe without a telescope---naked eye astronomy (note to Jesse Helms and Sen. Exon: that means astronomy without the use of a telescope). You just need to observe the objects carefully and notice how things change over time. The vocabulary terms are in boldface.
Even though it is now known that this ancient model of a stationary Earth is incorrect, you can still use this model because it is a convenient way to predict the motions of the stars and planets relative to a location on the Earth. A star's apparent brightness is actually determined by its distance, as well as, its physical size and temperature. It is also now known that the stars apparent motion around us is due to the Earth rotating once every 24 hours on its axis. The stars are stationary and the Earth rotates from west to east. This rotational motion makes the stars appear to move from east to west around us. The celestial sphere model is used by planetaria to simulate the night sky. I hope you will be able to distinguish between the convenience of the celestial sphere model and the way things really are.
Why a sphere? The Earth is spherical! This was known much earlier than Columbus' time. Sailors had long known that as a ship sailed away from the shore it not only diminished in apparent size, but it also appeared to sink into the water. The simplest explanation to use was that the Earth was curved (particularly, since those ships did come back without falling off some edge!). They also knew that if one traveled in a north-south direction, some stars disappeared from view while others appeared. The difference in the height of a star's height above the north or south horizon is directly proportional to the difference in the north-south distance of observers looking at the star at the same time. The simplest explanation said that the Earth is round, not flat. Pythagoras noted that the shadow of the Earth falling on the Moon during a lunar eclipse was always curved and the amount of the curvature was always the same. The only object that always casts a circular shadow regardless of its orientation is a sphere. This Pythagorean argument is passed on to us through the writings of Aristotle.
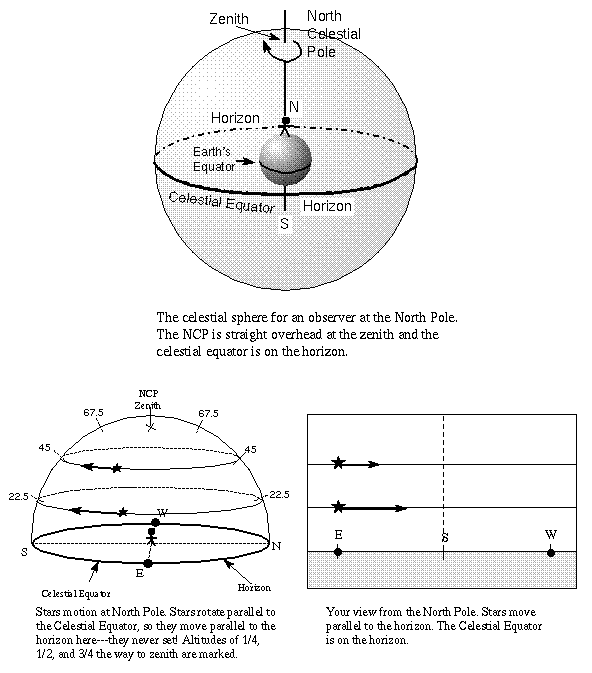
If you joined Santa last Christmas at the north pole (90 degrees latitude), you would have seen Polaris straight overhead and the celestial equator on your horizon. The point straight overhead on the celestial sphere for any observer is called the zenith and is always 90 degrees from the horizon. The arc that goes through the north point on the horizon, zenith, and south point on the horizon is called the meridian. The positions of the zenith and meridian with respect to the stars will change as the celestial sphere rotates and if the observer changes locations on the Earth, but those reference marks do not change with respect to the observer's horizon. Any celestial object crossing the meridian is at its highest altitude (distance from the horizon) during that night (or day). The angle the star paths make with respect to the horizon = 90 degrees - (observer's latitude).
During daylight, the meridian separates the morning and afternoon positions of the Sun. In the morning the Sun is ``anti meridiem'' (Latin for ``before meridian'') or east of the meridian, abbreviated ``a.m.''. At local noon the Sun is right on the meridian (the reason why this may not correspond to 12:00 on your clock is discussed a little later in this chapter). At local noon the Sun is due south for northern hemisphere observers and due north for southern hemisphere observers (though observers near the Earth's equator can see the local noon Sun due north or due south at different times of the year for reasons given in the next section). In the afternoon the Sun is ``post meridiem'' (Latin for ``after meridian'') or west of the meridian, abbreviated ``p.m.''.
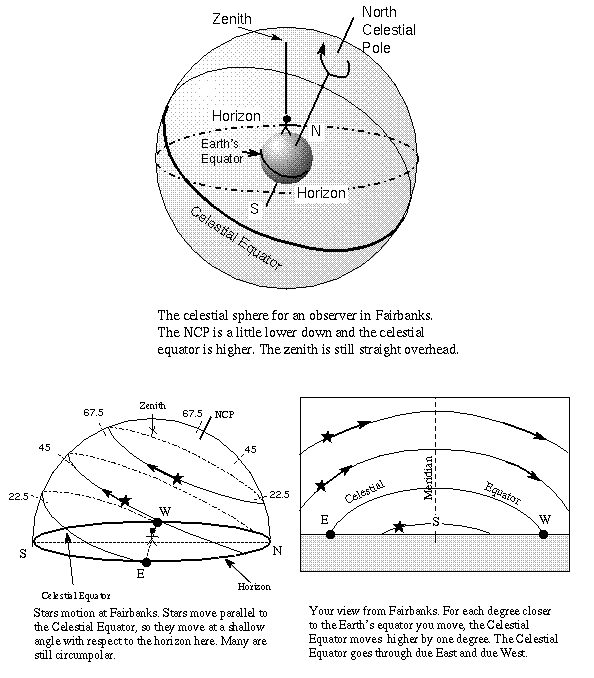
For each degree you move south with Santa in his sleigh, the North Celestial Pole (NCP from here on) moves 1 degree away from the zenith toward the north and the highest point of the celestial equator's curved path in the sky moves up one degree from the southern horizon. This effect has nothing to do with the distance between a celestial object or marker and you at different points on the Earth (remember that the celestial sphere has a practically infinite radius). In fact, observers on a spherical world only ten miles across would see the same effect! The picture above shows the celestial sphere for the far northern city of Fairbanks in Alaska. Since it is 25ƒ south of the north pole, the NCP is 25ƒ away from (north of) the zenith for Fairbanks observers.
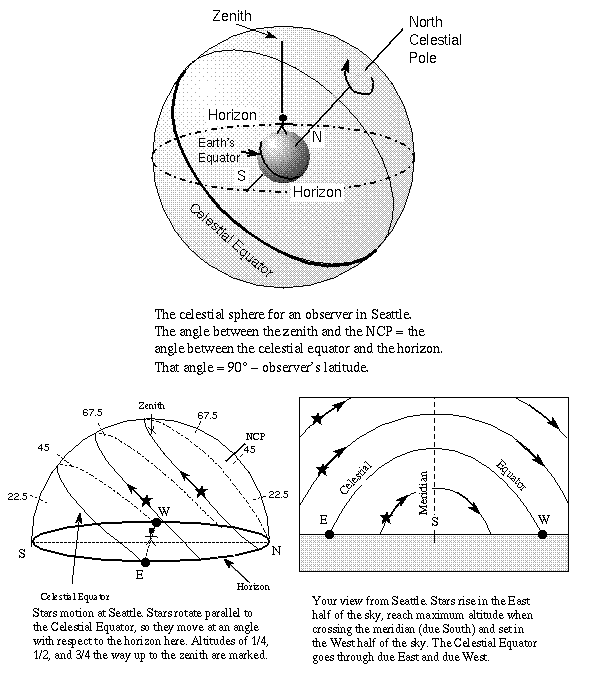
By the time you reach your hometown, the NCP has moved away from the zenith so it is now a number of degrees above the horizon equal to your latitude on the Earth. Remember that your position on the Earth is specified by a latitude and a longitude coordinate. The latitude is the number of degrees north or south of the Earth's equator. On a map or globe, lines of latitude run horizontally, parallel to the equator. The longitude is the number of degrees east or west of the 0ƒ longitude line (the ``prime meridian'' on the Earth) that runs through Greenwich England. On a map or globe, lines of longitude run vertically, perpendicular to the equator. The celestial sphere for observers in Seattle and any other observer at the same latitude (47ƒ N) on the Earth is shown above.
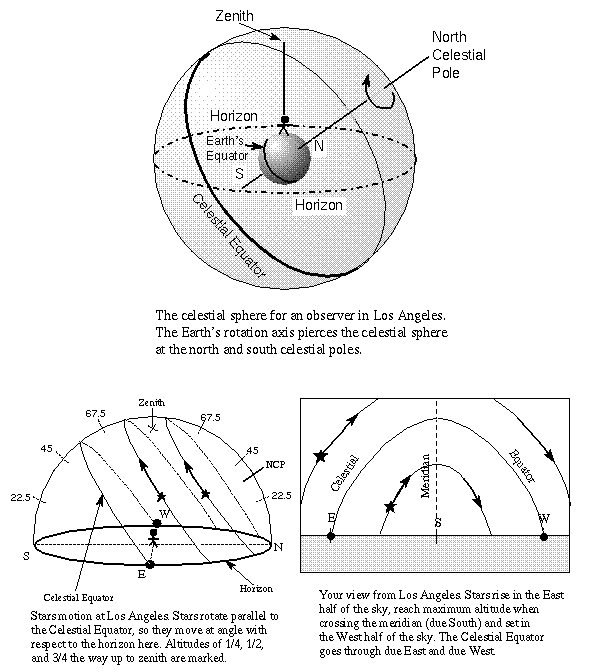
For another more detailed example, let's choose Los Angeles at latitude 34ƒ N. The NCP is therefore 34 degrees above the north horizon. The diagram for latitude 34ƒ N is shown above. Notice that finding the angle of the NCP above the horizon provides a very easy way of determining your latitude on the Earth (a fact used by navigators even today!). Because the Earth's equator is 90ƒ away from the north pole, the celestial equator as seen in Los Angeles will arc up to 90 - 34 = 56 degrees above the southern horizon at the point it crosses the meridian. It still intercepts the horizon at the exactly east and west points. The stars rise in the east part of the sky, move in arcs parallel to the celestial equator reaching maximum altitude when they cross your meridian, and set in the west part of the sky. The star paths make an angle of 90 - 34 = 56 degrees with respect to the horizon.
If you are in the northern hemisphere, celestial objects north of the celestial equator are above the horizon for more than 12 hours because you see more than half of their total 24-hour path around you. Celestial objects on the celestial equator are up 12 hours and those south of the celestial equator are above the horizon for less than 12 hours because you see less than half of their total 24-hour path around you. The opposite is true if you are in the southern hemisphere.
Notice that stars closer to the NCP are above the horizon longer than those farther away from the NCP. Those stars within an angular distance from the NCP equal to the observer's latitude are above the horizon for 24 hours---they are circumpolar stars. Also, those stars close enough to the SCP (within a distance = observer's latitude) will never rise above the horizon. They are also called circumpolar stars.
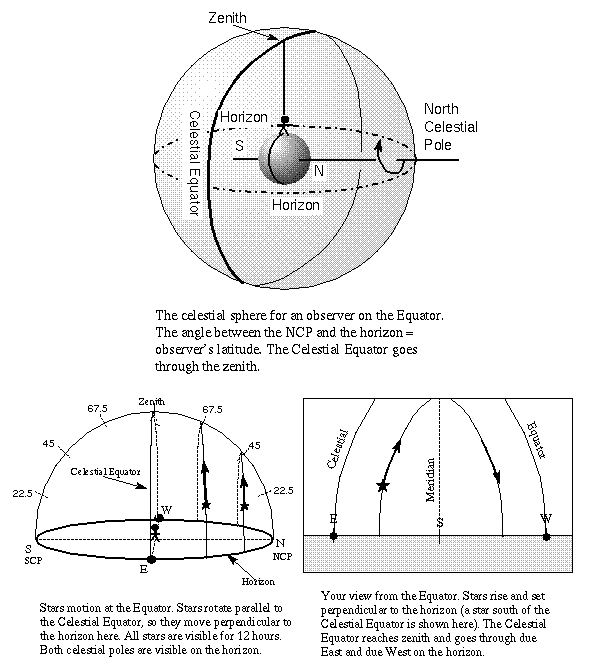
To warm Rudolph's frozen nose, Santa heads down to the equator (0 degrees latitude). At the equator, you see the celestial equator arcing from exactly east to the zenith to exactly west. The NCP is on your northern horizon. At the equator you see one-half of every star's total 24-hour path around you so all stars are up for 12 hours. All of the stars rise and set perpendicular to the horizon (at an angle = 90 - 0 = 90 degrees).
Continuing southward you see the NCP disappear below the horizon and the SCP rise above the southern horizon one degree for every one degree of latitude south of the equator you go. The arc of the celestial equator moves to the north, but the arc still intercepts the horizon at the exactly east/west points.
Here is a summary of the positions of the celestial reference marks (note that ``altitude'' means the number of degrees above the horizon):
| celestial equator | circumpolar | latitude |
|---|---|---|
| longitude | meridian | North Celestial Pole |
| South Celestial Pole | zenith |
Furthermore, the Sun appears to drift eastward with respect to the stars (or lag behind the stars) over a year's time. It makes one full circuit of 360 degrees in 365.24 days (very close to 1 degree or twice its diameter per day). This drift eastward is now known to be caused by the motion of the Earth around the Sun in its orbit.
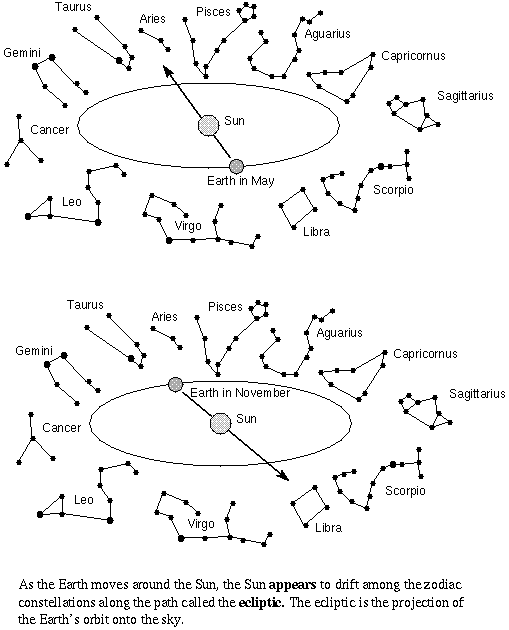
The apparent yearly path of the Sun through the stars is called the ecliptic. This circular path is tilted 23.5 degrees with respect to the celestial equator because the Earth's rotation axis is tilted by 23.5 degrees with respect to its orbital plane. Be sure to keep distinct in your mind the difference between the slow drift of the Sun along the ecliptic during the year and the fast motion of the rising and setting Sun during a day.
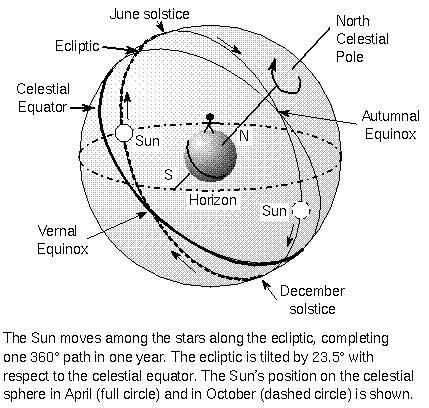
The ecliptic and celestial equator intersect at two points: the vernal (spring) equinox and autumnal (fall) equinox. The Sun crosses the celestial equator moving northward at the vernal equinox around March 21 and crosses the celestial equator moving southward at the autumnal equinox around September 22. When the Sun is on the celestial equator at the equinoxes, everybody on the Earth experiences 12 hours of daylight and 12 hours of night for those two days (hence, the name ``equinox'' for ``equal night''). The day of the vernal equinox marks the beginning of the three-month season of spring on our calendar and the day of the autumn equinox marks the beginning of the season of autumn (fall) on our calendar. When the Sun is above the celestial equator during the seasons of spring and summer, you will have more than 12 hours of daylight. When the Sun is below the celestial equator during the seasons of autumn and winter, you will have less than 12 hours of daylight.
Make sure you understand this. No matter where you are on the Earth, you will see 1/2 of the celestial equator's arc. Since the sky appears to rotate around you in 24 hours, anything on the celestial equator takes 12 hours to go from exact east to exact west. Every celestial object's diurnal (daily) motion is parallel to the celestial equator. So for northern observers, anything south of the celestial equator takes less than 12 hours between rise and set, because most of its rotation arc around you is hidden below the horizon. Anything north of the celestial equator takes more than 12 hours between rising and setting because most of its rotation arc is above the horizon. For observers in the southern hemisphere, the situation is reversed. However, remember, that everybody anywhere on the Earth sees 1/2 of the celestial equator so at the equinox, when the Sun is on the equator, you see 1/2 of its rotation arc around you, and therefore you have 12 hours of daylight and 12 hours of nightime everyplace on the Earth.
The geographic poles and equator are special cases. At the geographic poles the celestial equator is right along the horizon and the full circle of the celestial equator is visible. Since a celestial object's diurnal path is parallel to the celestial equator, stars do not rise or set at the geographic poles. On the equinoxes the Sun moves along the horizon. At the North Pole the Sun ``rises'' on March 21st and ``sets'' on September 22. The situation is reversed for the South Pole. On the equator observers see one half of every object's full 24-hour path around them, so the Sun and every other star is above the horizon for exactly 12 hours for every day of the year.
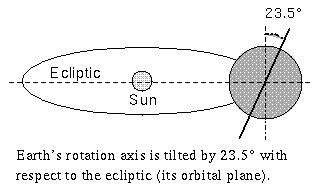Since the ecliptic is tilted 23.5 degrees with respect to the celestial equator,
the Sun's maximum angular distance from the celestial equator is 23.5 degrees.
This happens
at the solstices. For observers in the northern hemisphere, the farthest
northern point above the celestial equator is the summer solstice, and
the farthest southern point is the winter solstice.
The word ``solstice'' means ``sun standing still'' because the Sun stops moving northward
or southward at those points on the ecliptic. The Sun reaches
winter solstice around December 21 and you see the least part of its diurnal
path all year---this is the day of the least amount of daylight and marks the
beginning of the season of winter for the northern hemisphere. The Sun
reaches the summer solstice around June 21 and you see the greatest part of its
diurnal path above the horizon all year---this is the day of the most amount of daylight
and marks the beginning of the season of summer for the
northern hemisphere. The seasons are opposite for the southern hemisphere (eg.,
it is summer in the southern hemisphere when it is winter in the northern
hemisphere). The Sun
does not get high up above the horizon on the winter solstice. The Sun's rays hit
the ground at a shallow angle at mid-day so the shadows are long. On the summer
solstice the mid-day shadows are much shorter because the Sun is much higher above
the horizon.
| autumnal (fall) equinox | ecliptic | season |
|---|---|---|
| solar day | summer solstice | vernal (spring) equinox |
| winter solstice |
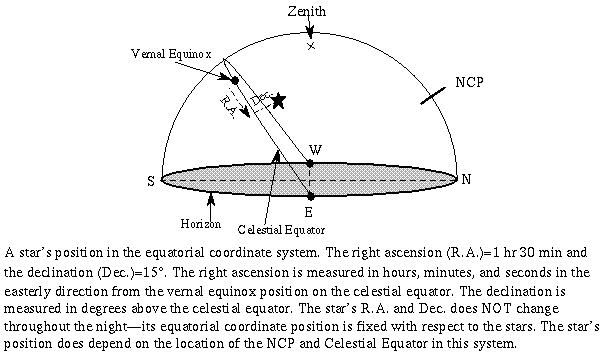
There are a couple of popular ways of specifying the location of a celestial object. The first is what you would probably use to point out a star to your friend: the altitude-azimuth system. The altitude of a star is how many degrees above the horizon it is (anywhere from 0 to 90 degrees). The azimuth of a star is how many degrees along the horizon it is and corresponds to the compass direction.
Azimuth starts from exactly North = 0 degrees azimuth and increases clockwise: exactly East = 90 degrees, exactly South = 180 degrees, exactly West = 270 degrees, and exactly North = 360 degrees = 0 degrees. For example, a star in the southwest could have an azimuth between 180 degrees and 270 degrees. Since stars change their position with respect to your horizon throughout the night, their altitude-azimuth position changes. Also, observers at different locations looking at the same star at the same time will see it at a different altitude-azimuth position. A concise summary of this coordinate system and the numbers involved is given at the end of this section.
The second way of specifying star positions is the equatorial coordinate system. This system is very similar to the longitude-latitude system used to specify positions on the Earth's surface. This system is fixed with respect to the stars so, unlike the altitude-azimuth system, a star's position does not depend on the observer's location or time. Because of this, astronomers prefer using this system. You will find this system used in astronomy magazines and in most sky simulation computer software.
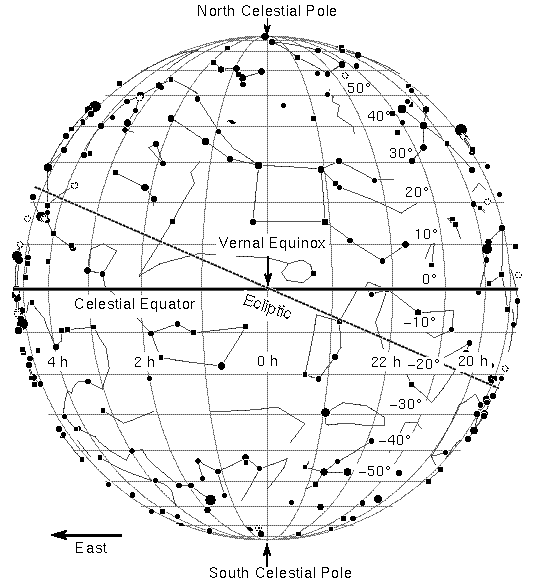
The lines on a map of the Earth that run north-south are lines of longitude and when projected onto the sky, they become lines of right ascension. Because the stars were used to measure time, right ascension (RA) is measured in terms of hours, minutes, and seconds instead of degrees and increases in an easterly direction. Zero RA is where the Sun crosses the celestial equator at the vernal equinox. The full 360 degrees of the Earth's rotation is broken up into 24 hours, so one hour of RA = 15 degrees of rotation. The lines of RA all converge at the celestial poles so two stars one hour of RA apart will not necessarily be 15 degrees in angular separation on the sky (only if they are on the celestial equator will they be 15 degrees apart). For two stars one hour of RA apart and that are not circumpolar, you will see one star rise one hour before the other. If they were 30 minutes of RA apart, you would see one rise half an hour before the other, etc.
The lines on a map of the Earth that run east-west parallel to the equator are lines of latitude and when projected onto the sky, they become lines of declination. Like the latitude lines on Earth, declination (dec) is measured in degrees away from the celestial equator, positive degrees for objects north of the celestial equator and negative degrees for objects south of the celestial equator. Objects on the celestial equator are at 0 degrees dec, objects half-way to the NCP are +45 degrees, objects at the NCP are +90 degrees, and objects at the SCP are -90 degrees. Polaris's position is at RA 2hr 31min and dec 89 degrees 15 arc minutes. A concise summary of this coordinate system and the numbers involved is given at the end of this section.
An effect called precession causes the Sun's vernal equinox point to slowly shift westward over time, so a star's RA and dec will slowly change by about 1.4 degrees every century (a fact ignored by astrologers), or about 1 minute increase in a star's RA every twenty years. This is caused by the gravitational pulls of the Sun and Moon on the Earth's equatorial bulge (from the Earth's rapid rotation) in an effort to reduce the tilt of the Earth's axis with respect to the ecliptic and the plane of the Moon's orbit around the Earth (that is itself slightly tipped with respect to the ecliptic). Like the slow wobble of a rapidly-spinning top, the Earth responds to the gravitational tugs of the Sun and Moon by slowly wobbling its rotation axis with a period of 26,000 years.
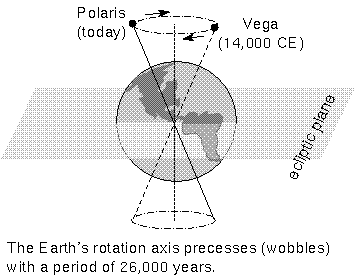
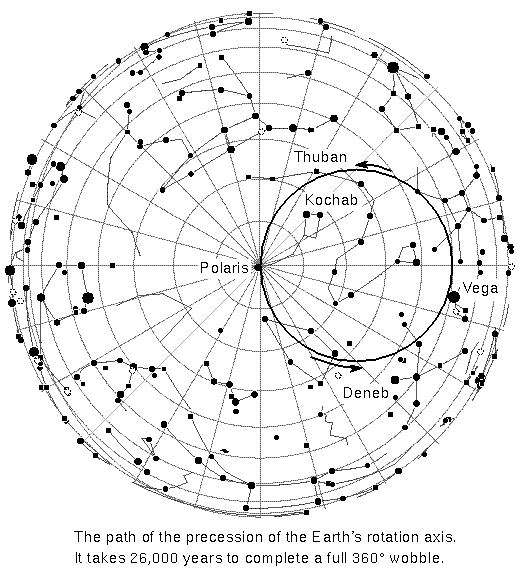
This motion was first recorded by Hipparchus in 100 B.C.E. who noticed differences between ancient Babylonian observations and his own. When the Babylonians were the world power in 2000 B.C.E., the vernal equinox was in the constellation Aries and the star Thuban (in Draco) was the closest bright star to the NCP. At the time of Jesus Christ the vernal equinox had shifted to the constellation Pisces and the star Kochab (in the bowl of the Little Dipper) was the closest bright star to the NCP. Now the star Polaris is close to the NCP and the vernal equinox is close to the border between Pisces and Aquarius (in 2600 C.E. it will officially be in Aquarius) which is what a popular song of years ago refers to with the line ``this is the dawning of the Age of Aquarius''. In the year 10,000 C.E., the bright star in the tail of Cygnus, Deneb, will be the pole star and Vega (in Lyra) will get its turn by the year 14,000 C.E. Horoscopes today are still based on the 4,000-year old Babylonian system so even though the Sun is in Aries on my birthday, the zodiac sign used for my horoscope is Taurus. I guess it's hard to keep up with all of the changes in the modern world!
| altitude | azimuth | declination |
|---|---|---|
| precession | right ascension |
Go to Time
and Seasons section
last update: 25 January 1999
(661) 395-4526
Bakersfield College
Physical Science Dept.
1801 Panorama Drive
Bakersfield, CA 93305-1219