Stars are hundreds of thousands of times farther away from us than the planets are from us. The nearest star (other than the Sun) is so far away that the fastest spacecraft the human race has built so far would take almost 100,000 years to get there. Yet we are a curious and ambitious species, and we want to know how those stars are born, live out their lives, and die. How can we learn about objects that are so remote and beyond our physical grasp? This chapter gives you an idea of how we learn about the stars and what we find about the stars. If your math skills are rusty, study the math review appendix and do not hesitate to ask your astronomy instructor for help. The vocabulary terms are in boldface.
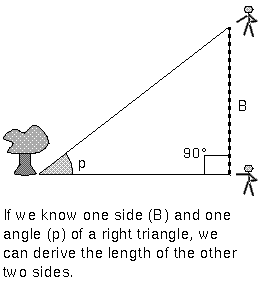
A favorite way to measure great distances is a technique used for thousands of years: look at something from two different vantage points and determine its distance using trigonometry. The object appears to shift positions compared to the far off background when you look at it from two different vantage points. The angular shift, called the parallax, is one angle of a triangle and the distance between the two vantage points is one side of the triangle. Basic trigonometric relations between the lengths of the sides of a triangle and its angles are used to calculate the lengths of all of the sides of the triangle. This method is called trigonometric parallax. Modern surveyors use this method to measure great distances, so the method is sometimes called ``the surveyor's method''.

The side of the triangle between the observers, labelled ``B'' in the figure above, is called the baseline. The size of the parallax angle p is proportional to the size of the baseline. If the parallax angle is too small to measure because the object is so far away, then the surveyors have to increase their distance from each other. Ordinarily, you would have to use trigonometric functions like a tangent or a sine, but if the angle is small enough, you find a very simple relation between the parallax angle p, baseline B, and the distance d:
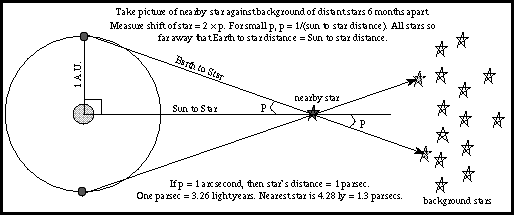
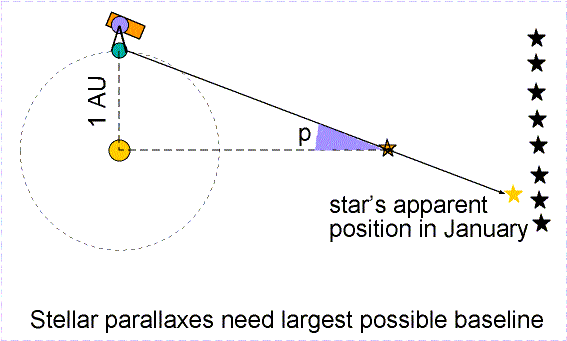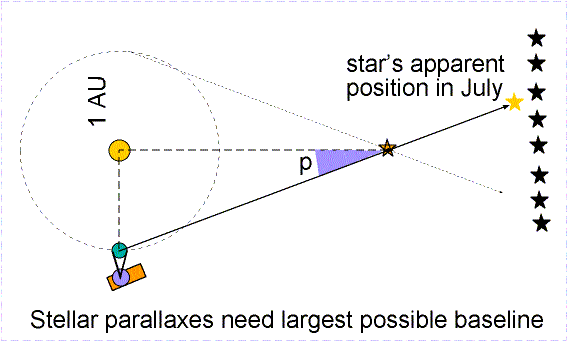
Trigonometric parallax is used to measure the distances of the nearby stars. The stars are so far away that observing a star from opposite sides of the Earth would produce a parallax angle much, much too small to detect. As large a baseline as possible must be used. The largest one that can be easily used is the orbit of the Earth. In this case the baseline is the distance between the Earth and the Sun---an astronomical unit (AU) or 149.6 million kilometers! A picture of a nearby star is taken against the background of stars from opposite sides of the Earth's orbit (six months apart). The parallax angle p is one-half of the total angular shift.
However, even with this large baseline, the distances to the stars in units of astronomical units are huge, so a more convenient unit of distance called a parsec is used (abbreviated with ``pc''). A parsec is the distance of a star that has a parallax of one arc second using a baseline of 1 astronomical unit. Therefore, one parsec = 206,265 astronomical units. The nearest star is about 1.3 parsecs from the solar system. In order to convert parsecs into standard units like kilometers or meters, you must know the numerical value for the astronomical unit---it sets the scale for the rest of the universe. Its value was not know accurately until the early 20th century (see the planetary science chapter). In terms of light years, one parsec = 3.26 light years.
Which unit should you use to specify distances: a light year or a parsec? Both are fine and are used by astronomers (including myself) all of the time, just as you may use ``feet'' and ``yards'' in everyday talk. However, when the parsec unit is used on this web site, the equivalent in light years will usually be given as well, but when the light year unit is used, the parsec equivalent will usually not be given. Using a parsec for the distance unit and an arc second for the angle, our simple angle formula above becomes extremely simple:
Shifts as small as 1/50 arc second can be measured from the surface of the Earth. This means distances can be determined for stars that are up to 50 parsecs away. If a star is further away than that, its parallax angle p is too small to measure and you have to use more indirect methods to determine its distance. Stars are about a parsec apart from each other on average, so the method of trigonometric parallax works for just a few thousand nearby stars. Recently, the Hipparcos mission completed its work to extend the database of trigonometric parallax distances. Exquisitely precise instruments were put on board a satellite orbiting the Earth to get above the blurring effects of the atmosphere. It measured the parallaxes of 118,000 stars to an astonishing precision of 1/1000 arc second (about 20 times better than from the ground)! It measured the parallaxes of 1 million other stars to a precision of about 1/20 arc seconds. Selecting the Hipparcos link will take you to the Hipparcos homepage and the catalogs.
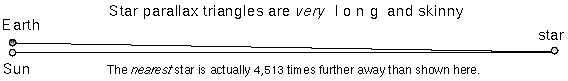
The actual stellar parallax triangles are much longer and skinnier than the ones typically shown in astronomy textbooks. They are so long and skinny that you do not need to worry about which distance you actually determine: the distance between the Sun and the star or the distance between the Earth and the star. Taking a look at the skinny star parallax triangle above and realizing that the triangle should be over 4,500 times longer (!), you can see that it does not make any significant difference which distance you want to talk about. But if you are stubborn, consider these figures:
| the Sun--nearest star distance = | 267,068.230220 AU = | 1.2948 pc; |
| the Earth--nearest star distance = | 267,068.230222 AU = | 1.2948 pc; |
| Pluto--nearest star distance = | 267,068.233146 AU = | 1.2948 pc! |
If you are super-picky, then yes, there is a slight difference but no one would complain if you ignored the difference. For the more general case of parallaxes observed from any planet, the distance to the star in parsecs d = ab/p, where p is the parallax in arc seconds, and ab is the distance between the planet and the Sun in AU.
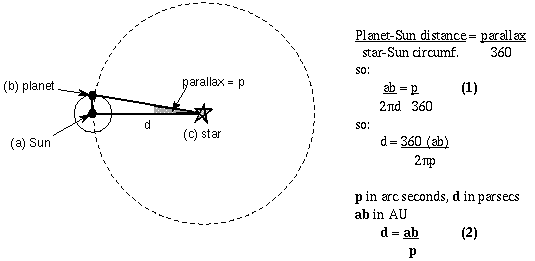
Formula (1) relates the planet-Sun baseline distance to the size of parallax measured. Formula (2) shows how the star-Sun distance d depends on the planet-Sun baseline and the parallax. In the case of Earth observations, the planet-Sun distance ab = 1 A.U. so d = 1/p.
| astronomical unit | parsec | trigonometric parallax |
|---|
A star's apparent brightness (its flux) decreases with the square of the distance. The flux is the amount of energy reaching each square centimeter of a detector (eg., your eye, CCD, piece of the sphere) every second. Energy from any light source radiates out in a radial direction so concentric spheres (centered on the light source) have the same amount of energy pass through them every second. As light moves outward it spreads out to pass through each square centimeter of those spheres.
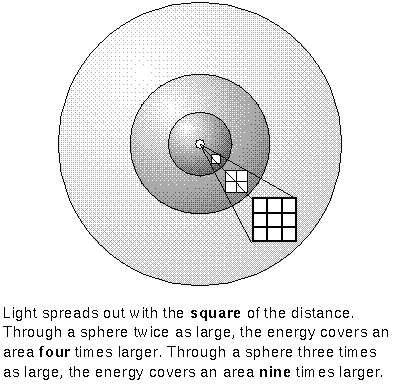
The same total amount of energy must pass through each sphere surface. Since a sphere has a surface area of 4p × (its radius)2, the flux of energy on sphere-1 = (the flux of energy on sphere #2) × [(sphere #2's radius)/(sphere #1's radius)]2. Notice that the radius for the reference flux (sphere #2) is on the top of the fraction while the radius for the unknown flux (sphere #1) is on the bottom---this is an inverse square law! As the distance INcreases, the flux DEcreases with the square of the distance. See the math review appendix for help on when to multiply and when to divide the distance factor.
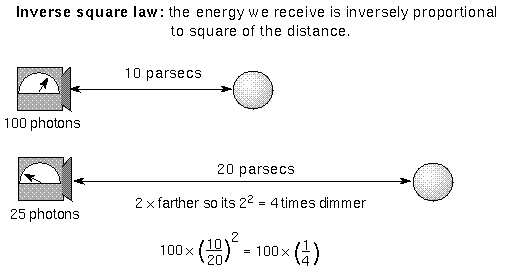
Put another way: As the flux DEcreases, the star's distance INcreases with the square root of the flux. If you know how much energy pours through the star's surface and you measure how much energy you detect here on the Earth, then you can derive the star's distance from you.
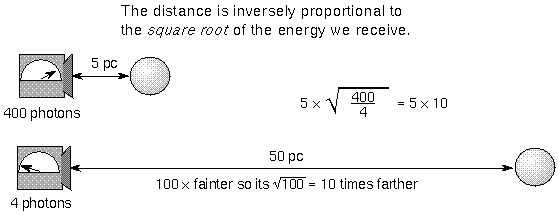
| flux | Inverse Square Law of Light Brightness |
|---|
![]() Go to Magnitude System section
Go to Magnitude System section
last update: 26 February 1999
(661) 395-4526
Bakersfield College
Physical Science Dept.
1801 Panorama Drive
Bakersfield, CA 93305-1219