History and Philosophy of Western Astronomy
Full window version
(looks a little nicer). Click <Back> button to get back to
small framed version with content indexes.
This chapter covers the development of western astronomy
and modern science. I focus on the rise of modern science in Europe, from the
ancient Greeks to Isaac Newton. Other cultures were also
quite interested and skilled in astronomy (the
Mayans,
Egyptians, peoples of
India and China come immediately to mind), but the Greeks were the first ones
to try to explain how the universe worked in a logical, systematic manner
using models and observations. Modern astronomy has its roots in the Greek
tradition.
An excellent resource I used to construct these notes is
Science and the Human Prospect by Ronald Pine. These notes will be in
outline form to aid in
distinguishing various concepts. The vocabulary terms are italicized.
-
- By the 7th Century B.C.E. a common viewpoint had arisen in Greece
that the Universe is a rational place following universal,
natural laws and we are able to figure out those laws. Open inquiry and
critical evaluation was highly valued. The emphasis was on the process of
learning about the universe rather
than attaining the goal. But people eventually got tired of learning and wanted
absolute answers. Science is not able to
give absolute, certain answers. There
was disagreement among the experts and there came to be a crisis in confidence
that led to the rise of the Sophists.
-
- The Sophists taught that truth and morality are myths; relative to the
individual. Since truth and morality are just cultural inventions, a person should
conform to the prevailing views, rather than resolutely holding to some belief as
an absolute one.
-
- Socrates (lived 470-399 B.C.E.) taught that we can attain real truth through
collaboration with others. By exploring together and being skeptical about ``common
sense'' notions about the way things are, we can get a correct understanding of
how our world and society operate.
-
- Plato (lived 427-347 B.C.E., a student of Socrates) taught that there are absolute
truths---mathematics is the key. While statements about the physical world will be
relative to the individual and culture, mathematics is independent of those
influences: 2 + 2 = 4 always, here on Earth or on the far side of the galaxy.
Plato had Four Basic Points:
- There is certainty.
- Mathematics gives us the power of perception.
- Though the physical applications of mathematics may change, the thoughts
themselves are eternal and are in another realm of existence.
- Mathematics is thought and, therefore, it is eternal and can known by anyone.
[Today we view mathematical ideas as free creations of the human mind. They are the
tools we use to map the world. Experience is the key. Although absolute certainty
is not possible, we can still attain accurate knowledge and reasonable beliefs
about the world.]
-
- Out of Plato's teachings grew the belief that when one studies mathematics,
one studies the mind of God. Mathematical symmetries are the language of universal design and
harmony. Their faith in order caused the Greeks to try to find explanation for
the seemingly unordered planets (particularly
retrograde motion). Their faith
in an ordered universe compelled them to make precise observations and they
were sustained by their belief in the power of reason. In one form or another
modern scientists have
this faith in an ordered universe and the power of
human reason.
-
- The Greeks were guided by a paradigm that was first articulated by Pythagoras.
A paradigm is a general consensus of belief of how the world works. It is
a mental framework we use to interpret what happens around us.
The Pythagorean Paradigm had three key points about the movements
of celestial objects: 1) Their motion is perfectly circular; 2) Their motion is
perfectly uniform; and 3) The Earth is at the exact center of their motion.
Plato gave his students a major problem to work on. Their task was to find a
geometric explanation for the apparent motion of the planets, especially
the strange retrograde motion. One key observation: as a planet undergoes
retrograde motion, it becomes brighter. They were, of course, also guided by the
Pythagorean Paradigm. This meant that regardless of the scheme they came up with,
the Earth should be at the unmoving center of the planet motions. One student named
Aristarchus violated that rule and developed a model with the Sun at the center.
His model was not accepted because of the obvious observations against a moving
Earth.
-
- Some of the observations that convinced the Greeks that the Earth was
not moving are
- The Earth is not part of the heavens.
- The celestial objects are bright points of light while the Earth is an
immense, nonluminous sphere of mud and rock.
- There is little change in the heavens---stars are the same night after night.
In contrast to this, the Earth is home of birth, change, and destruction. The
celestial bodies have an immutable regularity that is never achieved on the
corruptible Earth. Today we know that
stars are born and eventually die (some quite spectacularly!)---the length of
their lifetimes are much more than a human lifetime so they appear unchanging.
Also, we know today that the stars do change positions with respect to each other
over, but without a telescope, it takes hundreds of years to notice the changes.
- Our senses show Earth is stationary:
- a.
- Air, clouds, birds, and other things unattached to Earth are not left
behind as they would be if the Earth was moving. There would be a strong wind
if the Earth were spinning as suggested by some radicals. There is no strong wind.
- b.
- If the Earth were moving, then anyone jumping from a high point would hit
the Earth far behind from the point where the leap began. Today we have the
understanding of inertia and forces that explains why this does not happen even
though the Earth is spinning and orbiting the Sun.
- c.
- Rocks, trees, and people would be hurled from a rotating Earth. They
knew about centrifugal force, but they did not know about the force of gravity and
inertia.
-
- Plato taught that since an infinite number of
theories can be constructed to account for the observations, we can never empirically answer
what the universe is really like. He said that should adopt an instrumentalist
view: scientific theories are just tools or calculation devices and are not to
be interpreted as real. Any generalizations we make may be shown to be false in the future
and, also, some of our false generalizations can actually ``work''--an
incorrect theory can explain the observations (see the
scientific method page for background
material on this).
-
- Aristotle (lived 384-322 B.C.E.) was a student of Plato and had probably the
most significant influence on many fields of studies (science, theology, philosophy,
etc.) of any single person in history. He thought that Plato had gone too far with
his instrumentalist view of theories. Aristotle taught a realist view:
scientific, mathematical tools are not merely tools---they characterize the way the
universe actually is. At most one model is correct. The model he chose was
Eudoxus' crystalline spheres because:
- Most popular and observational evidence supported it (see item A above).
- His physics and theory of motion necessitated a geocentric
(Earth-centered) universe. In his theory of motion things naturally move to the
center of the Earth and
the only way to deviate from that is to have a force applied to the object.
- Agreed with the Pythagorean paradigm of uniform, circular motion (see item
F of the previous section above).
-
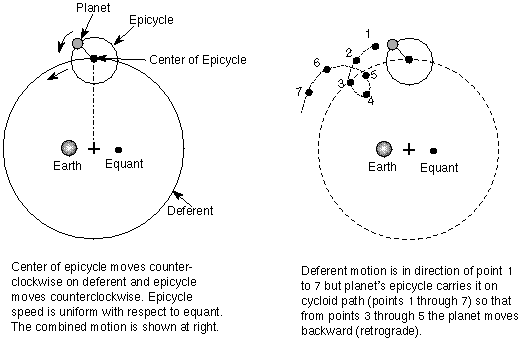
- Ptolemy (lived 85-165 C.E.) greatly extended Apollonius' and Hipparchus' models which used epicycles (a planet had a smaller circular
motion--an epicycle--around a point that was itself in a circular orbit around
the Earth; see the figure below). Epicycles were an important part of the model
and explained why the planets
are brighter as they retrogress. He added some refinements to explain the
details of the observations:
- Eccentrics--true center of planet motion (not the Earth!)
- Equant--planet moves uniformly in relation to it (not the Earth!)
These refinements are incompatible with Aristotle model and the Pythagorean paradigm--a
planet on an epicycle would crash into its crystalline sphere and the motion is
not truly centered on the Earth. So he adopted an instrumentalist view--this strange
model is only an accurate calculator to predict the planet motions but the
reality is Aristotle's model. Ptolemy was successful in having people adopt his
model because he gathered the best model pieces together, used the most
accurate observations and he published his work.
-
- By the 16th century the following paradigm had developed: Man is God's
special creation of the physical
universe; the Earth is the center of a mathematically planned universe and we
are given the gift of reading this harmony. The Greek ideal of finding logical,
systematic explanations to physical events was rediscovered and celebrated.
Along with this came an unbounded faith in the power of reason to solve
physical problems.
-
- Scientists use a guiding principle called Occam's Razor to choose
between two or models that accurately explained the observations. This
principle, named after the English philosopher, William
of Occam, who stated this principle in the mid-1300's, says:
the best model is the simplest one---the one requiring the fewest
assumptions and modifications
in order to fit the observations. Guided by Occam's Razor some scientists
began to have serious doubts about Ptolemy's geocentric model in the early days
of the Renaissance.
-
- Nicolaus Copernicus (lived 1473--1543 C.E.) found
many deficiencies in the Ptolemaic model. He felt that any model of the planet
motions must account for the observations and have circular, uniform motion.
The Ptolemaic model did not do
that. Also, the Ptolemaic model was not elegant and, therefore, un-Godlike.
During the years between Ptolemy and Copernicus, many small epicycles
had been added to the main epicycles to make Ptolemy's model agree with the
observations. By Copernicus' time, the numerous sub-epicycles and offsets had
made the Ptolemaic model very complicated. Surely, God would have made a
cleaner more elegant universe!
Copernicus was strongly influenced by neoplatonism (beliefs that combined elements of Christianity and Platonism) in developing a model to replace
Ptolemy's. This led him to:
- believe that the Sun is a material copy of God---God is the creative force
sustaining life and the Sun gives us warmth and light; and
- adopt Aristarchus' heliocentric (Sun-centered) model because God
should be at the center. Copernicus' model had
same accuracy as the revised Ptolemaic one but was more elegant.
Copernicus retained the Aristotelian notion that planets were striving to
fulfill the goal of perfect (circular) motion. His model still used small
epicycles to get the details of the retrograde loops correct, though they were
only a minor feature. He used trigonometry to describe the distances of the
planets from the Sun relative to the astronomical unit (average
Earth-Sun distance), but he did not know the numerical value of the AU. He
found that the
planets farther from the Sun move slower. The different speeds of the planets
around the Sun provided a very simple explanation for the observed retrograde
motion.
Retrograde motion is the projected position of a planet on the
background stars as the Earth overtakes it (or is passed by, in the case of the
inner planets). The figure below illustrates this. Retrograde motion is just an
optical illusion! You see the
same sort of effect when you pass a slower-moving truck on the highway. As you
pass the truck, it appears to move backward with respect to the background
trees and mountains. If you continue observing the truck, you'll eventually see
that the truck is moving forward with respect to the background scenery. The
relative geometry of you and the other object determines what you see projected
against some background.
Copernicus thought his model was reality but other people accepted his model as
a more convenient calculation device only. If the Earth were moving around the
Sun, then the stars
should appear to shift due to our looking at them from different vantage
points in our orbit (a ``parallactic shift'').
No
parallactic shift was observed in stars. If there was actually a very small
parallactic shift, then
the stars would have to be very far away. Copernicus' contemporaries
felt that God would not waste that much space! They argued that, therefore, there must be no parallactic shift at all---the Earth is not in motion. We
now know that the stars are indeed very far away and we must use telescopes to
detect the small parallactic shifts.

-
- Tycho Brahe (lived 1546-1601 C.E.) revived Heroclides' model that had the all of the planets, except the stationary Earth,
revolving around the Sun. The Sun, Moon, and stars revolve around the Earth.
Tycho's model was mathematically equivalent to Copernicus' model but did not
violate Scripture and common sense. Brahe was not a neoplatonist.
Tycho calculated that if the Earth moved, then the stars are at least
700 times farther away from
Saturn than Saturn is from Sun. Since Tycho believed that God would not waste that
much space in a harmonious, elegant universe, he believed that the Earth was at
the center of the universe. We now know that the nearest star is over
28,500 times farther away than Saturn is from the Sun!
Though Tycho's beliefs of the universe did not have that much of an effect on
those who followed him, his exquisite observations came to play a key role in
determining the true motion of the planets by Johannes Kepler. Tycho was
one of the best observational astronomers to have ever lived. Without using a
telescope, Tycho was able to
measure the positions of the planets to within a few arc minutes---a
precision and accuracy never before obtained by naked eye observers (at least
ten times better!).
Vocabulary
| astronomical unit | epicycle | geocentric |
| heliocentric | instrumentalism | Occam's Razor |
| paradigm | Pythagorean paradigm | realism |
retrograde motion |
- What two basic kinds of models have been proposed to explain the
motions of the planets?
- What is the Ptolemaic model? What new things did Ptolemy add to his
model?
- Why are epicycles needed in Ptolemy's model?
- Why was the Ptolemaic model accepted for > 1000 years?
- What is the Copernican model and how did it explain retrograde motion?
- Why did Copernicus believe in his model?
- Did he know the absolute distance between various planets and the Sun in
his model?
- What important contributions did Tycho Brahe make to astronomy?
-
- In the 16th century the hierarchical structure of the Church's authority
was inextricably bound with the geocentric cosmology.
- ``Up'' meant ascension to greater perfection and greater control.
- God and heaven existed outside the celestial sphere. There was a
gradation of existence and control from perfect existence to the central
imperfect Earth.
- God delegated power to angels to control the planet movements and to
guide the various earthly events.
- Plants and animals existed to serve humans and humans were to serve God
through the ecclesiastical hierarchy of the Church.
-
- Giordano Bruno (lived 1548--1600 C.E.) revived
Democritus' view that the Sun was
one of an infinite number of stars. This infinite sphere was consistent with
the greatness of God. Bruno believed in a heliocentric universe. Bruno
believed that God gives each of us an
inner source of power equal to all others, so there was no justification for
domination and servitude. His model had definite political ramifications that
threatened the church's political authority.
-
- Galileo Galilei (1564-1642 C.E.): 1609 points the telescope to the sky (the telescope was originally used as a naval tool to assess the strength of
the opponent's fleet from a great distance). He finds new things:
- New stars never seen before (makes Bruno's argument more plausible).
- Pits and craters on the Moon and spots on the Sun. This meant that the
Earth is not only place of change and decay!
- Four moons orbiting Jupiter. These four moons (Io, Europa, Ganymede, and
Callisto) are called the Galilean satellites in his honor. In this system
Galileo saw a mini-model of the heliocentric system. The moons are not
moving around the Earth but are centered on Jupiter. Perhaps other objects,
including the planets, do not move around the Earth.
- Venus goes through a complete set of phases. The gibbous and full phases
of Venus are impossible in the Ptolemaic model but possible in Copernican model
(and Tychonic model too!). In the Ptolemaic model Venus was always
approximately between us and the Sun and was never found further away from the
Earth than the Sun. Because of this geometry, Venus should always be in a
crescent, new, or quarter phase. The only way to arrange Venus to make a
gibbous or full phase is to have it further away from us than the Sun. This was
possible only if Venus orbited the Sun. For Galileo the clear observations of
a heliocentric universe was a powerful weapon against the hierarchical
structure.
Galileo argued that the heliocentric model is not a mere instrument but is
reality. His experiments showed that. His ideas not derived from thought/reason alone
but used the guidance of nature (experiments). Galileo is often considered the father of modern
science because his ideas were not derived from thought and reason alone.
He used the guidance of nature (experiments). This marked a revolutionary
change in science---observational experience became the key method for
discovering nature's rules.
-
- The struggle between Galileo and the Church was not a battle between
science and religion but was part of a larger battle over different conceptions
of the proper routes to knowledge, God, and world view.
-
- Galileo loved to debate and had the bad habit
of ridiculing those he disagreed with. Some of those were powerful political
figures in the Church. He wrote a book detailing the arguments for and against
his model of the universe in a way that ridiculed the official view of the
Church. It was written in Italian (the language of everyday discourse) rather
than the scholarly Latin so even non-scholars were exposed to his scathing
arguments against the geocentric universe. He may have had more success in
getting greater acceptance of his different views of God and research if his
style was different but perhaps his ideas needed just such a champion at that
time.
- What important contributions did Galileo make to modern science?
- What were his astronomical discoveries and why was he able to make those
discoveries?
- Why did he get into political hot water?
- What observation finally disproved the Ptolemaic model?
- Why is Galileo sometimes referred to as the first ``modern scientist''?
-
- Johannes Kepler (lived 1571--1630 C.E.) was hired
by Tycho Brahe to work out the mathematical details of Tycho's version of the
geocentric universe. Kepler was a religious
individualist. He did not go along with the Roman Catholic Church or the
Lutherans. He has an ardent mystical neoplatonic faith. He wanted to work with
the best observational data available because he felt that elegant, mathematically
harmonious theories must match reality. Kepler was motivated by his faith in
God to try to discover God's plan in the universe---to ``read the mind of God.''
Kepler shared the Greek view that mathematics was the language of God. He knew that
all previous models were inaccurate, so other scientists had not yet ``read the
mind of God.''
-
- Since an infinite number of models are possible (see
Plato's Instrumentalism above),
he had to choose. Although he was
hired by Tycho to work on Tycho's geocentric model, Kepler did not believe in
either Tycho's model or Ptolemy's model (he thought Ptolemy's model was
mathematically ugly). His neoplatonic faith led him to choose Copernicus'
heliocentric model.
-
- Kepler tried to refine Copernicus' model. After
years of failure, he was
finally convinced with great reluctance of an revolutionary idea: God uses a
different mathematical
shape than the circle. This idea went against the 2,000 year old Pythagorean
paradigm of the perfect shape being a circle! Kepler had a hard time convincing
himself that planet orbits are not circles and his contemporaries, including the
great scientist Galileo, disagreed with Kepler's conclusion. Planetary orbits
are ellipses with the Sun at one focus.

An ellipse is a
squashed circle that can be drawn by punching two thumb tacks into some paper,
looping a string around the tacks, stretching the string with a pencil, and moving
the pencil around the tacks while keeping the string taut. The figure traced out
is an ellipse and the thumb tacks are at the two foci of the ellipse. An oval shape
(like an egg) is not an ellipse: an oval tapers at one end, but an ellipse is
tapered at both ends (Kepler had tried oval shapes but he found they did not work.)
There are some terms we will use a lot in the rest of
this course that are used in discussing any sort of orbit. Here is a list of
definitions:
- Major axis---the length of the longest dimension of an ellipse.
- Semi-major axis---one half of the major axis and equal to the distance
from the center of the ellipse to one end of the ellipse. It is also the average
distance of a planet from the Sun at one focus.
- Minor axis---the length of the shortest dimension of an ellipse.
- Perihelion---point on a planet's orbit that is closest to the Sun. It
is on the major axis.
- Aphelion---point on a planet orbit that is farthest from the Sun. It
is on the major axis directly opposite the perihelion point. The aphelion +
perihelion = the major axis.
- Focus---one of two points along the major axis such that the distance
between it and any point on the ellipse + the distance between the other focus
and the same point on the ellipse is always the same value. The Sun is at one of
the two foci (nothing is at the other one). The Sun is NOT at the center of the
orbit!
- (a)
- As the foci are moved farther apart from each other, the ellipse becomes more
eccentric (longer and skinnier).
- (b)
- A circle is a special form of an ellipse that has the two foci at the same
point (the center of the ellipse).
- The eccentricity (e) of an ellipse = 1 -
(perihelion)/(semi-major axis). Circles have an eccentricity = 0; very long and
skinny ellipses have an eccentricity close to 1 (a straight line has an
eccentricity = 1).
- (a)
- The semi-minor axis = semi-major axis ×
Sqrt[(1 - e2)].
- (b)
- Planet orbits have small eccentricities (nearly circular orbits) which is why
astronomers before Kepler thought the orbits were exactly circular. This slight
error in the orbit shape accumulated into a large error in planet positions after
a few hundred years. Only very
accurate and precise observations can show the elliptical character of the orbits.
Tycho's observations, therefore, played a key role in Kepler's discovery and is an
example of a fundamental breakthrough in our understanding of the universe being
possible only from greatly improved observations of the universe.
- (c)
- Most comet orbits have large eccentricities (some are so eccentric that the
aphelion is around 100,000 AU while the perihelion is less than 1 AU!).
The figure below illustrates how the shape of an ellipse depends on the
semi-major axis and the eccentricity. Notice where the Sun
is for each of the orbits. The eccentricity of the ellipses increases from top
left to bottom left in a counter-clockwise direction in the figure.

-
- To account for the planets' motion (particularly Mars') among the stars,
Kepler found that the planets must move around the Sun at a variable speed.
When the planet was close to perihelion, it moved quickly; when
it was close to aphelion, it moved slowly. This was another break with the
Pythagorean paradigm of uniform motion! The Sun-planet radius vector sweeps
out equal areas in equal times.
Later, scientists found that this is a
consequence of the conservation of
angular momentum. The angular
momentum of a planet is a measure of the amount of orbital motion it has and does
NOT change as the planet orbits the Sun. It equals
the (planet mass) × (planet speed) × (distance from the Sun). If the distance
decreases, then the speed must increase to compensate; if the distance increases,
then the speed decreases (a planet's mass does not change).
-
- Finally, after several more years of
calculations, Kepler found a simple, elegant equation relating the distance of
a planet from the Sun to how long it takes to orbit the Sun (the planet's orbital
period). (One planet's sidereal period/another planet's sidereal
period)2
= (one planet's average distance from Sun/another planet's average distance
from Sun)3 OR
(sidereal period in years)2
= (semimajor axis of orbit in A.U.)3.
For example, Mars' orbit has a semi-major axis of 1.52 A.U., so 1.5243
= 3.54 and this equals 1.882. The number 1.88 is the number of years it
takes Mars to go around the Sun.
This simple mathematical
equation explained all of the observations throughout history and proved to Kepler
that the heliocentric system is real. Actually, the first two laws were sufficient,
but the third law was very important for Newton and is used today to determine the
masses of many different types of celestial objects (see
the gravity applications page for several
examples). We are going to use Kepler's third law a lot in this course!

Vocabulary
| angular momentum | aphelion | eccentricity |
| ellipse | focus | Kepler's 1st law |
| Kepler's 2nd law | Kepler's 3rd law | perihelion |
| semi-major axis |
- What shape are planet orbits and where is the Sun with respect to the orbit?
- What happens to a planet's orbital speed as it
approaches its farthest point from the Sun and as it approaches its
closest point? How is it related to angular momentum?
- How were Kepler's laws of planetary motion revolutionary or a radical break
from earlier descriptions of planetary motion?
- A moon's closest distance from a planet is 300,000 km and its farthest
distance is 500,000 km. What is the semi-major axis of its elliptical
orbit?
- How will the semi-minor axis compare with the semi-major axis for an ellipse
with eccentricity = 0.1, 0.5, 0.8, 0.99? (Find the value of semi-minor/semi-major).
- How will the perihelion compare with the aphelion for an ellipse with
eccentricity = 0.1, 0.5, 0.8, 0.99? (Find the value of perihelion/aphelion).
- How is the average distance between a planet and the Sun related to the
planet's orbit period?
- Which planet has a shorter period--one with a large average distance, or
one with a small average distance?
- What is the semi-major axis of an asteroid orbiting the Sun with a period of
64 years? (Kepler's third law works for any object orbiting the Sun.)
-
- Often a mathematical idea or model is discovered with no apparent application
to the physical world until many years later. This aspect of pure, basic
scientific research is not popular among government officials who want practical
applications NOW! How are scientific discoveries made? There are several views
about how we make discoveries and why humans are able to do this.
-
- Is there a creationary resonance between the human mind and the laws of
nature?
Kepler believed that God creates humans with the gift of reading the mathematical
harmonies of God's mind. It is only a matter of time for someone to discover
God's plan.
-
- Is there an evolutionary resonance between the human mind and the laws
of nature? This is a
modern view held by some that says, given the infinite experiments of evolution, it
is inevitable that creatures will eventually evolve capable of reading the laws
of nature. In this view, scientific progress is inevitable.
-
- Is creativity actually a logical process in disguise? Most people today
believe one's religious/philosophical beliefs are merely along for the
inevitable revolutionary ride and are not necessary to make
revolutionary scientific advances. Others believe that there are many technically
capable paths by which the universe can be modeled. Kepler's Neoplatonism was
not logically necessary for the discovery of the planetary laws of motion, but,
historically, it may have been absolutely necessary at his time and place.
-
- Every age has its paradigms. Though we try to be objective, philosophical
considerations do intrude on the scientific, creative process. That is not a bad
thing because these beliefs are crucial in providing direction to
our inquiries and fuel for our creativity mill. We have faith that there is some
order in the universe and this faith keeps us striving to solve the cosmic
problems.
-
- Facts have little meaning without ideas to interpret them. Because science is
a human discipline, there is no machine-like
objectivity. Often crucial facts supporting an idea come after a commitment is made
to the idea. So is science then all based on an individual's whim; relative to the
scientist's time and place?
-
- The self-corrective enterprise of
science is messier than most science textbooks would have you believe. Besides the
inevitable cultural prejudices, scientists have, in principle, an infinite number
of conceivable ideas to choose from. How do we separate reasonable ideas from the
infinite number of merely conceivable ideas?
-
- Reality kicks back. Sure, there are cultural biases, but science
does make us confront the real world---reality kicks back. We can ignore the
discrepancies between nature's truth (observations) and our theories of what should
happen only for so long. Experiments are the sole
judge of scientific truth---nature eventually wins. Our ideas are crucial to
understanding the world but they eventually yield to the facts. Science makes us
confront the world.
-
- Isaac Newton (lived 1641--1727 C.E.) was
probably the most brilliant scientist who ever lived. His greatest contributions
were in all branches of physics. Kepler's discoveries about elliptical orbits and
the planets' non-uniform
speeds made it impossible to maintain the idea of planetary motion as a natural one
requiring no explanation. Newton had to answer some basic questions: What keeps the
planets in their elliptical orbits? On our spinning Earth what prevents objects
from flying away when they are thrown in the air? What keeps us from being hurled
off the spinning Earth?
-
- The notion of a greater God and an infinite universe with no special places
leads to RenČ Descartes' (lived 1596-1650 C.E.) idea of inertia: body at rest
remains at rest, and one moving in a straight line maintains constant speed
and same direction unless deflected by a ``force''. Newton took this as the
beginning of
his description of how things move, so this is now known as Newton's 1st law of
motion. Note that this description of a force is different from the definition
of a force given by Aristotle. A force causes a change in something's
motion (an acceleration).
- An acceleration is a change in the speed and/or direction of motion.
Something at rest is not accelerating and something moving at constant speed in
a straight line is not accelerating.
- Something moving at a constant speed in a circular orbit (or any curved path)
IS accelerating---its direction is changing.
- A rock in your hand is moving horizontally as it spins around the center of
the Earth, just like you
and the rest of the things on the surface are. If you throw the rock straight up,
there is no change in its horizontal motion because of its inertia. You
changed the rock's vertical motion because you applied a vertical force
on it. The rock falls straight down because the Earth's gravity acts on only
the rock's vertical motion. If the rock is thrown straight up, it does not
fall behind you as the Earth rotates. Inertia and gravity also explain why we do
not feel a strong wind as the Earth spins---as a whole, the atmosphere is spinning
with the Earth.
- Newton's 1st law is a qualitative one---it tells us when something will
accelerate. His 2nd law quantifies the amount of change produced from a given
force---it enables us to calculate the amount of acceleration there will be.
-
- Isaac Newton finds that the amount of
force needed to produce a given amount of acceleration of an object of a given mass
is force = mass × acceleration (Newton's 2nd law).
-
- Newton completes his theory of dynamics with his third law of motion:
every force ON a body by some object has an equal and opposite force exerted BY that
body on the object (in a closed system). For
example, if you jump out of a boat into a lake, you will push on the boat and
it will move backward. At the same time, the boat pushes you forward. Another
example is seen when you walk. The Earth pushes your feet forward because your feet
are pushing the Earth backward. The Earth is much, much more massive than you are,
so its acceleration is much, much less than yours (using Newton's 2nd law).
-
- Using Kepler's third law and his 2nd law, Newton finds that the attractive
force, called gravity, between a planet and Sun a distance d apart is Force
= kp × (planet mass) /
(d)2, kp is a number that is the
same for all the planets. In the same way he finds that the gravity between the
Sun an a planet is Force = ks × (Sun mass) /
(d)2. Using
his 3rd law of motion, Newton derives his gravity force law: Fgrav
= G × (Sun mass) × (planet mass) /
(distance between them)2. Spherically
symmetric objects (eg., planets, stars, moons, etc.) behave as if all of their mass
is concentrated at their centers. So when we use Newton's Law of Gravity, we measure
the distance between the centers of the objects.
In a bold, revolutionary step, Newton found that his gravity law worked for
any two objects with mass---it applies for any motions on the Earth as well
as any motions in space. He unified celestial and terrestrial physics and completed
the process started by Copernicus. His law of gravity also explains Kepler's 1st and
2nd laws.
-
- Newton's development
of the unifying law of gravity is also the culmination of a process of Occam's
Razor in action. From Ptolemy to Newton, the theories of how the planets move
got simpler and more powerful as time went on. Ptolemy's model had become
extremely complicated by the time of the Renaissance and Copernicus reduced the
number of circular motions to around 50 so that it was simpler. Kepler vastly
simplified the theory of planet motion by reducing the number of essential parts
to just three laws. Newton unifed all of those laws to the ONE unifying law of
gravity. This law was so simple and elegant that it could also explain motions on
the Earth.
-
- But what is gravity? Newton understood how the
gravity force affected the motion of objects but not why gravity worked the way it
did. Recognizing the limits of his knowledge, he adopted an
instrumentalist view: the scientist's job is to capture observations in precise
mathematical equations; explain the ``how'' not the ``why''. Only things
verified by our experience of the world are admissible into science. Though the
``why'' question is intriguing and a few scientists will spend years trying to
answer it, most scientists share Newton's instrumentalist view.
-
- With Newton, there was no longer a
hierarchical-teleological universe (one designed by God for some purpose with man
playing a crucial role in the plan). The universe was now a perfect machine, based
on mathematics, set in motion by God
long ago. God is the reference point for absolute space and time. Newtonian
mechanics requires an absolute coordinate system to keep things sensible (this
also gives God something to do).
-
- A major change occurred in how people viewed the
world around them. Reality was completely reduced to material objects.
Ideas, thought, feelings, and values were secondary. Newtonism undercut the
role of God and religion and the validity of science: science became just a
subjective perspective of the machine universe.
Descartes saw the need to rescue thoughts, ideas and
values. He developed a mind-body dualism: a world of thought and spirit exists
independent of, but parallel to, the material world. There is a correspondence
between the God-inaugurated, mathematical thoughts of scientists and the
motions in the physical world. Descartes said that mathematical ideas work so
well because there is a pre-established parallelism between the physical world
and the human mind. What is real does not depend on us---this is probably
the actual completion of the Copernican revolution and is soon called ``common
sense'' (how about that for a paradigm shift!).
Vocabulary
| acceleration | inertia | Newton's 1st law |
| Newton's 2nd law | Newton's 3rd law | Newton's Law of Gravity |
- What 2 things can change for an acceleration?
- If you give a bowling ball a push FAR away from any gravitational effects,
what will it do? If you throw a feather (again far out in space) at the same
speed as the bowling ball, how will its speed compare to the bowling ball
after 5 minutes?
- Let's say you're twirling a ball on a string and the string breaks. What
path does the ball take and why is that?
- How do we know gravity acts on an orbiting satellite?
- How does a force exerted on an object relate to the object's mass or
acceleration? Given the same force will a boulder accelerate more than a
regular marble?
- Why would you need to apply more force to a bowling ball or a feather (far
out in space) so that they
would be travelling at the same speed after 10 minutes?
- What important discoveries and ideas did Newton make?
- What basic fundamental assumption did Newton make about the laws of
nature on the Earth and in space?
- How does Occam's Razor relate to the progress of planet motion theory
from Ptolemy to Newton?
-
- Gravity is one of four fundamental forces in nature---forces that cannot be
described in terms of any other forces and are responsible for every physical
interaction in the universe. The four fundamental forces in nature are:
- Strong nuclear---short range (only within the atomic nucleus) and
the strongest of the forces. It holds the atomic nucleus together. It is
1042 times stronger than gravity.
- Weak nuclear---weaker and also short range (nucleus range). It is responsible
for the decay of nuclei (radioactivity). It is 1029 times stronger than
gravity.
- Electromagnetic---electric and magnetic fields are aspects of the same
thing (first shown by James Maxwell who lived 1831-1879 C.E.). It can be attractive
or repulsive, it has an infinite range, it only works for things with charge and
it is much stronger than gravity: 1040 times stronger than gravity. If
we had two equal piles of just 325 kg of electrons on the near side of Moon and
Earth, their electrical repulsion would be enough to overcome the gravity binding
the 5.98 × 1024 kg Earth and 7.35 × 1022 kg Moon!
- Gravity---weakest of all of the forces but is important for astronomy
because:
- a.
- All atoms feel it whether they are charged or not (most of the material in
the universe is neutral overall, so the electromagnetic force does not affect it);
- b.
- It does not depend on the chemical composition of the material;
- c.
- It is always attractive, never repulsive; and
- d.
- It depends only on the number of atoms (mass) and the distance---it is
additive (more mass means more gravity) and it has an infinite range.
It is quite remarkable that only four forces can explain all physical
phenomena everywhere in the universe. This means that we can actually determine the
inner workings of far away objects using terrestrial physics! Meteorites, cosmic
rays, solar wind, and moon rocks tell us that the same laws of physics observed
on the Earth are observed elsewhere. The best evidence for this universality
comes from light (electromagnetic radiation) arriving from the far reaches of
space bearing messages of the conditions of those far away places. See the section
in the introduction page about astronomy's
value in the scientific endeavor
for a fuller discussion of the universality of the laws of physics.
-
- Science reduces observations to the fundamental processes and unifies
the observations into an overarching theory. The
goal of science is to unify seemingly disjoint facts into a coherent whole or
framework. Might the four fundamental forces be manifestations of one super
force? James Maxwell showed that electricity and magnetism are simply
manifestations of the electromagnetic force. In the 1970s, the electromagnetic
and weak nuclear forces were found to be manifestations of the ``electroweak
force''---they behave in the same way at very high temperatures and energies. We
are trying to unify the strong nuclear force with the others---the theories are
called Grand Unification Theories (GUT's). The strong and electroweak forces
would behave in the same way at extremely high temperatures and energies. We are
also trying to merge gravity with the rest of the forces (super-GUT's, a name that
indicates some scientists are watching too many Saturday morning cartoons).
- What are the four fundamental forces of the physical universe? Give a
description of them and include
the effective distances and relative strengths for the forces in your
description.
- Why is gravity often the most important force in astronomical
interactions?
- How do we know that there are probably not any other fundamental forces?
- How do we know that the laws of physics on the Earth are the same throughout
the rest of the universe?
- How do we know that the laws of physics are the same throughout time?
- What things does gravity depend on?
- How does gravity vary with distance between objects and with respect to
what do we measure the distances?
- What would happen to the orbit of Io (one of Jupiter's moons) if all of
the Hydrogen and Helium in Jupiter were converted to Silicon and Oxygen?
- What would happen to the Earth's orbit if the Sun suddenly turned into a
black hole (of the same mass)? Why?
- What would antimatter do in a gravitational field?
- What important laws of planet motion can be derived from Newton's law
of gravity?
For further reading, here are some of my references that cover the development
of science using historical records. They also cover science's philosophical
underpinnings using the tools of philosophy.
- Owen Barfield Saving the Appearances pp. 46--54.
- Paul K. Feyerabend Galileo and the Tyranny of Truth in
The Galileo Affair: A Meeting of Faith and Science ed. Coyne, Heller,
Zycinski (Vatican City: 1985), pp. 155-166 and other papers from that symposium
held at the Vatican.
- George S. Johnston 1995, The Galileo Affair (Scepter Press:
Princeton, NJ). HTML version version available here.
- Thomas S. Kuhn The Copernican Revolution: Planetary Astronomy in the
Development of Western Thought (Cambridge, Mass: Harvard Univ. Press,
1957).
- Ronald Pine Science and the Human Prospect (Wadsworth Publ. Co:
Belmont, CA, 1989) esp. ch. 5: pp. 130-162.
- A prelude to Copernicus is Owen Gingerich's Scientific American
article Astronomy in the Age of Columbus Nov. 1992, pp. 100-105.
last updated 09 July 1997
Nick Strobel --
Email:
strobel@lightspeed.net
(805) 395-4526
Bakersfield College
Physical Science Dept.
1801 Panorama Drive
Bakersfield, CA 93305-1219
�



