

Determining the structure of our galaxy is not an easy task because the solar system is stuck inside the Galaxy and we can only look in all different directions. Our situation is like you having to determine the layout of your hometown from just looking out on your front porch (or back porch) and not being able to move even across the street. The fact that you see a narrow band of stars tells you that our galaxy is shaped like a thin disk. If we lived in a more spherical galaxy, the stars would be distributed more uniformily around the sky. There is a hint of a bulge in the direction of the Sagittarius constellation. Careful star counts and determining their distances shows hints of a spiral pattern in the disk. The interstellar dust limits our view a small section of the Galaxy. However, clear evidence of the spiral structure in the disk comes from the 21-cm line radiation discussed in the previous section.
Our galaxy, the Milky Way, is disk-shaped with spiral arms in the disk. It has an elliptical bulge in the center and a spherical halo that is denser closer to the Galaxy center. It is about 100,000 light years across and our solar system is about two-thirds of the way out from the center (for comparison, our solar system with the Oort Cloud is about 1 light year across). A view of the Galaxy as seen from above is shown at the top of this page. From the side the Galaxy would look very flat because most of the stars are in the disk (see the figure below).
You can make a rough guess of the number of stars in our galaxy by dividing the Galaxy's total mass by the mass of a typical star (e.g., 1 solar mass). The result is about 200 billion stars! The actual number of stars could be several tens of billions less or more than this approximate value. Recently, astronomers have discovered that most of the mass of the Galaxy (and other galaxies) is not in the form of stars, gas, or dust. It is made of some other material, as yet unknown, and is given the descriptive name ``dark matter''. Note that this affects your guess of the number of stars in the galaxy! (Does it increase the number or decrease it?)

Our galaxy probably closely resembles the galaxy NGC 891 as seen edge-on. Note the prominent dust lanes going through the disk mid-plane and how flat the galaxy is.

Some stars are very useful for finding distances to clusters and to other galaxies because they have a known luminosity that is large, so they can be seen from great distances away. Bright objects of a known luminosity are called standard candles (though, in our modern day we should perhaps call them ``standard bulbs''). Standard candle objects are used to measure large distances. The particular standard candle stars Shapley used are in the last stages of their life and pulsate by changing size. They are trying to re-establish hydrostatic equilibrium but the thermal pressure is out of sync with the gravitational compression. The expanding star overshoots the equilibrium point. Then gravity catches up and contracts the star. But gravity contracts the star beyond the equilibrium point. The thermal pressure increases too much and the cycle continues.

Astronomers had to wait a few years for Harlow Shapley to calibrate Leavitt's relation using Cepheids in our galaxy for which the distances could be determined. In the calibration process Shapley put actual values to the luminosity part of the period-luminosity relation. With a calibrated period-luminosity relation astronomers could use Cepheid variables as standard candles to determine the distances to distant clusters and even other galaxies.
Cepheids have pulsation periods of 1 to 50 days. In the 1950's astronomers found that there are two types of Cepheids:


Because the luminosity of Cepheids can be easily found from the pulsation period, they are very useful in finding distances to the galaxies in which they reside. By comparing a Cepheid's apparent brightness with its luminosity, you can determine the star's distance from the inverse square law of light brightness. The inverse square law of light brightness says the distance to the Cepheid = (calibration distance) × Sqrt[(calibration brightness)/(apparent brightness)]. Recall that brightnesses are specified in the magnitude system, so the calibration brightness (absolute magnitude) is the brightness you would measure if the Cepheid was at the calibration distance of 10 parsecs (33 light years). In some cases the calibration distance may be the already-known distance to another Cepheid with the same period you are interested in.
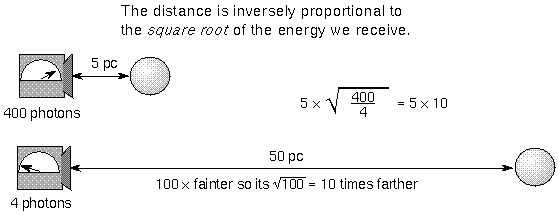
Early measurements of the distances to galaxies did not take into account the two types of Cepheids and astronomers underestimated the distances to the galaxies. Edwin Hubble measured the distance to the Andromeda Galaxy in 1923 using the period-luminosity relation for Type II Cepheids. He found it was about 90,000 light years away. However, the Cepheids he observed were Type I (classical) Cepheids that are about four times more luminous. Later, when the distinction was made between the two types, the distance to the Andromeda Galaxy was increased by about two times to about 2.3 million light years. Recent results from the Hipparcos satellite have given a more accurate distance of 2.93 million light years to the Andromeda Galaxy.


RR Lyrae are found in old star clusters called globular clusters and in the stellar halo part of our galaxy. All of the RR Lyrae stars in a cluster have the same average apparent magnitude. In different clusters, the average apparent magnitude was different. This is because all RR Lyrae have about the same average absolute magnitude (=+0.6, or 49 solar luminosities). If the cluster is more distant from us, the RR Lyrae in it will have greater apparent magnitudes (remember fainter objects have greater magnitudes!).
RR Lyrae stars can be used as standard candles to measure distances out to about 760,000 parsecs (about 2.5 million light years). The more luminous Cepheid variables can be used to measure distances out to 40 million parsecs (about 130 million light years). These distances are many thousands of times greater than the distances to the nearest stars found with the trigonometric parallax method. The method of standard candles (inverse square law) provides a crucial link between the geometric methods of trigonometric parallax and the method of the Hubble Law for very far away galaxies. (The Hubble Law is explained further later.)
 |  |
In the side view picture of the Galaxy above, the globular clusters are represented by the small circles congregating around the bulge of the Galaxy (they have been enlarged over a 100 times to make them visible). Shapley found a strong concentration of globular clusters in the direction of the constellation Sagittarius. In a continuation of the process started by Copernicus almost 500 years before, Shapley announced that our solar system is not at the center of the Galaxy!
If we were at the center of the Galaxy, we would see globular clusters equally distributed all around us. Instead, they congregate around some other point that Shapley calculated to be 32,600 light years from our solar system. He did not know about the dust in the interstellar medium. That discovery was made about a decade later. Now taking into account the effects of dust extinction on the brightnesses of stars and also that there are different types of Cepheids, astronomers find the solar system's distance to the center of the Galaxy is about 26,000 light years. Our position is slightly to the right of the arrow pointing to the disk in the side-view picture of the Galaxy above and is marked with the cross in the preceding top-view picture.
The gravity from the part of the Galaxy inside the star's orbit accelerates the star so it moves in an orbit. The greater the gravity pulling on a star, the faster the star will move. Applying the mass and orbit speed relations of the gravity chapter, the enclosed mass inside the star's orbit = (orbital speed)2 × (star's distance to the galactic center)/G, where G is the gravity constant. The Galaxy's mass is found from measuring the orbital speed of stars (or gas clouds) and their distance from the center.
From measurements of stars and hydrogen clouds in the galactic disk, astronomers construct a rotation curve for the Galaxy. This is a plot of the orbital speed of stars (or gas clouds) vs. their distance from the center of the Galaxy. The ``rotation'' part of the term refers to the motion of the disk as a whole. As a whole the disk seems to be rotating (spinning) even though it is really the individual stars and clouds that are orbiting around the center. The rotation curve tells you the the amount of mass inside a given distance from the center. You find how the mass is distributed in the Galaxy by looking at how the amount of enclosed mass changes with the size of the orbits.

A rigid body rotation is seen close to the center (as if the part close to the center was rotating as one single object even though it is made of stars and gas), then the curve drops off, then rises, and eventually flattens out as far out as can be seen. Because gravity becomes weaker with larger (increasing) distance, the stars on the outskirts of the visible galaxy should be moving slower than those closer to where most of the visible mass resides. Instead, they are moving at about the same speed, even though they are farther from most of the visible matter! There must be extra mass in the Galaxy we cannot see to create the extra amount of gravity force. The Galaxy is spinning too quickly---the visible matter does not have enough mass to keep the Galaxy together!
The observed rotation curve can be decomposed into the individual parts contributed by each component of the Galaxy: the disk, bulge + stellar halo, and the rest of total mass is what is called dark matter---material that does not emit any light (at least it is too faint to be detected yet) but has a significant amount of gravitational influence. The highest solid line in the left plot below is for all of the galactic components combined. The other curves (dashed, dotted, and solid) are the contributions of the individual galactic components (the bulge + stellar halo = ``bulge'', disk, and the dark matter halo) to the rotational velocity. In the figure below, the dark matter halo is called the ``corona''.

The plot on the right shows the enclosed mass inside a given distance. If you reach the point where the enclosed mass does NOT increase with distance, then you will have found the edge of the Galaxy's mass. Beyond the edge of the Galaxy, the rotational velocity will decrease as the distance from the center increases. Both plots show that the end of the Galaxy's mass has not yet been found! The stars, dust, and gas in the disk and stellar halo do not explain all the mass. The part of the Galaxy that fills up the remainder of mass is the dark matter halo (corona). Ninety percent of the Galaxy's mass is in the form of this dark matter! Unfortunately, because gravity depends only on the distance and mass and not the composition, astronomers are not certain what the dark matter is composed of. It could be in the form of planets, brown dwarfs (stars too small to shine from nuclear fusion), white dwarfs, black holes, neutrinos with mass, or other exotic particles that have not been discovered in the laboratory yet.
Some students have expressed skepticism about this dark matter. Are not astronomers going ``too far'' with their speculations? Scientists, by nature, are skeptical themselves of any radical change in our understanding of the universe. However, nature and careful observations are the sole judge of scientific truth and even the smartest scientist must yield to what nature is telling us. The conclusion that dark matter exists has come from using the standard scientific method of observation, interpretation, and testing of the explanation. Looking back in history, the detection of dark matter is just another application of Newton's law of gravity. Until Neptune was directly observed, its presence was known from its gravitational effect on Uranus (Neptune was ``dark matter''). Astronomers have used the orbits and wobbling of stars to detect the presence of as yet, unseen companions around them (i.e., planets and black holes). The extrasolar planets and black holes are technically, dark matter too. They may be faint or invisible themselves, but they produce definite gravitational effects on nearby visible objects. At the other end of the scale, no one has ever directly seen an electron, but you know such a particle exists and is essential to our society of electricity and electronics.
![]() Go to
Interstellar Medium and beginning of Galactic Structure sections
Go to
Interstellar Medium and beginning of Galactic Structure sections
![]() Go to
Spiral Arms section
Go to
Spiral Arms section
last update: 22 April 1999
(661) 395-4526
Bakersfield College
Physical Science Dept.
1801 Panorama Drive
Bakersfield, CA 93305-1219